Découverte des transformations affines, des systèmes de fonctions itérées, pour aboutir aux attracteurs et au magnifiques images qui en découlent. Construction d’une figure.
Introduction :
A l’aide d’un logiciel qui porte le nom de Mathematica, nous pouvons créer toutes sortes de figures. Parmi elles, nous pouvons dessiner des attracteurs de transformations affines.
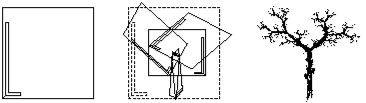
Voici des exemples de ces différentes créations :
- La fougère de Barnsley

- Un fractal
Comment en dessiner une ? Mais qu’est-ce donc que ces attracteurs et ces itérations de transformations affines ?
Pour comprendre ce qu’est une transformation affine itérée, il suffit simplement de prendre un ensemble de point (image, figure géométrique) et de le dupliquer mais en changeant sa taille, son angle, sa grosseur, etc. Itérer une fonction (ou plus exactement itérer la composition d’une fonction), signifie que l’on compose plusieurs fois la fonction avec elle-même. Itération est donc synonyme de répétition.
Les systèmes de fonctions itérées consistent en plusieurs fonctions qui sont itérées. Le théorème de Hutchinson dit que si chaque fonction est contractante alors il existe un attracteur et il est unique.
Cet attracteur est donc l’image suite à plusieurs transformations affines sur une image (fonction).
Résumons :
– On prend un objet
– On le déforme
– On le translate
– On le translate à nouveau, et encore, et encore, etc. (Le but étant de le translater un très grand nombre de fois pour pouvoir observer un attracteur)

(Ce triangle est noir, il est dépourvu d’attracteur)

(Triangle avec attracteurs. Les zones d’attractions sont en noir et théoriquement aucun point ne peut être dans les zones blanches)
Il n’est pas toujours possible de calculer avec précision le comportement d’un système composé d’un très grand nombre d’éléments qui interagissent. C’est pour cela que si on arrive à trouver un attracteur, alors on pourra, dans une certaine mesure, traiter le problème en travaillant sur celui-ci. Au final, un attracteur nous permettra de comprendre plus ou moins le mouvement d’un système sans pour autant avoir connaissance de sa trajectoire, mais juste avec le point d’arrivée de la trajectoire.
L’attracteur est pour ainsi dire un lieu vers lequel un système de fonction est
attiré.
Essayons maintenant de reproduire une figure
– Pour commencer, allez sur le site de Wolfram Project et grâce à la démonstration Fractal Creation with Iterated Function Systems que vous téléchargez, vous pouvez dessiner toutes sortes d’attracteurs de transformations affines en jouant avec les curseurs. (Attention, vous devez posséder le logiciel Mathematica player pour pouvoir le télécharger.)
Lorsque vous êtes satisfaits de votre œuvre, laissez la page ouverte ou enregistrez l’image.
Pour ma part, voici mon chef-d’œuvre ! (Mais je suis sûre qu’entre nous, c’est vous l’artiste !) :
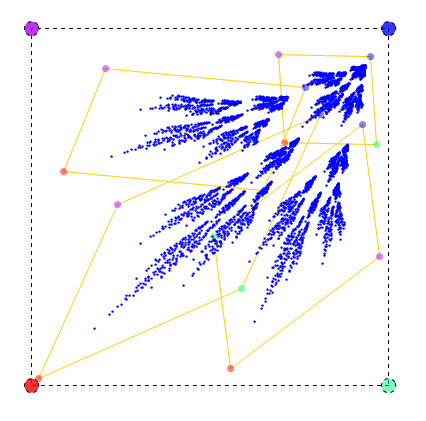
Le cours de dessin est maintenant terminé. Passons aux choses sérieuses…
– Avec Mathematica, nous allons reproduire cette figure.
– Mais avant toute chose :
Nous cherchons les coefficients d’une transformation affine à partir de points et de leurs transformés. Nous avons 6 inconnues, a, b, c, d pour la matrice et e, f pour la translation. L’expression de la transformation affine correspond à deux équations :
$u = ax + by + e$
$v = cx + dy + f$
Il y a six inconnues (coefficients de la transformation). Nous devons avoir 6 équations pour trouver les valeurs de ces inconnues. Nous allons résoudre ces 6 équations avec Mathematica. Il faut donc considérer 3 points et leurs images pour avoir 6 équations.
– Appelons (x1,y1),(x2,y2) et (x3,y3) les coordonnées des points originaux et (u1,v1),(u2,v2) et (u3,v3) les coordonnées des points de son image.
Nous avons donc bien 6 équations et 6 inconnues.
Vous n’avez rien compris à cette étape ? Ce n’est pas grave !
Vous connaissez les systèmes d’axes tout de même ?
- x : correspond à l’axe des abscisses
- y : correspond àl’axe des ordonnées
Bien !
– Sur ma figure on constate 4 parties. Ces parties sont délimitées par 4 petits points reliés. Ce sont ces 4 points qui nous intéressent. Mais seuls 3 nous sont nécessaires.
– En utilisant le fichier Mathematica ci-dessus, placez les valeurs pour x1, y1, x2, y2, x3, y3 en utilisant 3 des points de couleur du grand carré extérieur. C’est à vous de définir une échelle et à quels points de couleur vous souhaitez les associer. Étant donné que ces points sont la base, on garde ces mêmes valeurs lors du calcul de chaque partie.
– Ensuite placez les valeurs pour u1, v1, u2, v2, u3, v3 en utilisant l’une des parties et 3 de ces points de couleurs. Les couleurs correspondent aux 1, 2, et 3 des x, y, u et v, alors gardez toujours le même ordre. (Dans ma figure : (x1, y1) et (u1, v1) bleu / (x2, y2) et (u2, v2) turquoise / (x3, y3) et (u3, v3) rouge).
– Une fois les équations validées vous obtenez les solutions des 6 inconnues (a, b, c, d, e, f)
– Répétez cette étape avec les 3 autres parties.
– Au final vous obtenez 4x les valeurs a, b, c, d, e, f (toujours différent)
– Remplacez ces valeurs dans l’ordre des parties et alphabétique :
$m1 = {{a, b}, {c, d}}$
$q1= {{e, f}}$
– Recopiez le code (en veillant à avoir les mêmes notations)
– Pour finir, choisissez un nombre d’attracteur…
– Quand je valide le tout, voici mon résultat :

Conclusion :
À travers ces images, ces explications et cette construction, nous pouvons mieux comprendre le rôle de l’attracteur et de quelle manière on y aboutit. Comme son nom l’indique, il a la propriété d’attirer. Malgré que la théorie soit toujours un peu compliquée, il est intéressant de voir que des calculs peuvent aboutir à de magnifiques images et figures…

