On cherche à calculer expérimentalement la capacité c d’un condensateur, puis on compare cette valeur à celle fournie par la théorie.
par Emilien Stern, Gael Burkardt, Romain Muller
La charge q sur une plaque d’un condensateur est proportionnelle à la différence de potentiel V entre les plaques du condensateur, ce qui s’exprime par
q=CV d’où V=q/C
où C est une constante nommée capacité, mesurée en Farad [F].
Si un condensateur de capacité C est connecté à une résistance R[Ohms], un courant dépendant du temps s’établit. Ce courant varie exponentiellement lors de la charge ou de la décharge du condensateur.
Déroulement de l’expérience
– Objectifs :
- Mesurer la constante de temps d’un circuit RC.
- Comparer celle-ci à la valeur prévue (R fois C).
- Mesurer la différence de potentiel entre les plaques d’un condensateur en fonction du temps, à la charge et à la décharge.
- Ajuster une fonction aux données. L’un des paramètres correspond à une constante de temps expérimentale.
– Matériel :
- Ordinateur
- LabPro
- Logger Pro
- Sonde de tension Vernier
- Fils de connexion
- Condensateur non polarisé de 10 micro F
- Résistances de 100 kohm, 47 kohm
- Piles ou alimentation
- Commutateur

Questions préalables
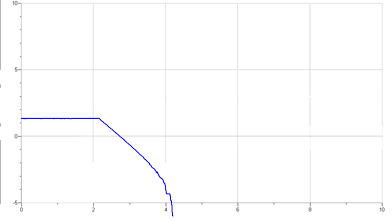
– Soit une boule de verre contenant des bonbons, avec 1000 bonbons au départ. Vous passez à côté une fois par heure. Comme vous voulez que personne ne remarque que vous prenez des bonbons, vous prenez à chaque fois 10% des bonbons restants dans la boule. Faites un graphique du nombre de bonbons restants pour les quelques premières heures. En bleu. Si vous enleviez 20% des bonbons, comment le graphique changerait-il ? Esquissez le nouveau graphique. En rouge.

Mesures
- Les paramètres d’ajustement ont étés déterminés grâce à LabPro, avec lequel nous avons observé la courbe du potentiel en fonction du temps (V(t)) lors de la charge ou de la décharge du condensateur. Puis nous avons cherché les meilleurs paramètres (A, B et c [1]) pour les fonctions d’ajustement.
| Paramètres d'ajustements | Résistance | Capacité | Constante de temps | ||||
| Essai | A | B | c | 1/C | R[kohms] | C[microF] | RC[s] |
| Décharge 1 | 22.64 | -0.062 | 1.1 | 0.91 | 100 | 10 | 1 |
| Charge 1 | 16.72 | -13.88 | 1.1 | 0.91 | 100 | 10 | 1 |
| Décharge 2 | 76.4 | 0.03 | 2.25 | 0.44 | 47 | 10 | 0.47 |
| Charge 2 | 100.7 | -97.76 | 2.25 | 0.44 | 47 | 10 | 0.47 |
– Graphiques obtenus :
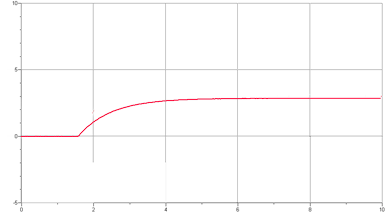
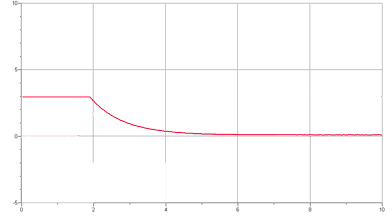

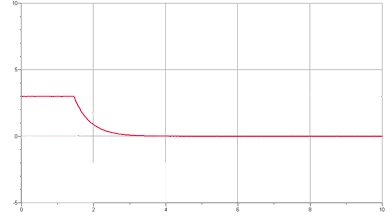
Analyse
– Comparez les valeurs expérimentales au modèle proposé pour la charge et la décharge du condensateur : quel est le lien entre le c obtenu expérimentalement et la constante de temps du circuit définie ci-dessous ?
-
-
- Charge : V(t)=V0e-t/RC
-
-
-
- Décharge : V(t)=V0(1-e-t/RC)
-
-
-
- Charge : V(t)=A*(1-e-c*t)+B
-
-
-
- Décharge : V(t)=A*e-c*t+B
-
- On peut donc en déduire que RC = 1/c, pour la charge et la décharge.
– Quel est l’effet de la diminution de la résistance sur la charge et la décharge du condensateur ?
- La charge et la décharge s’effectuent plus rapidement, conformément au modèle proposé.
– Quelle est la signification de la pente du graphique de ln(V) en fonction du temps pour la décharge ?
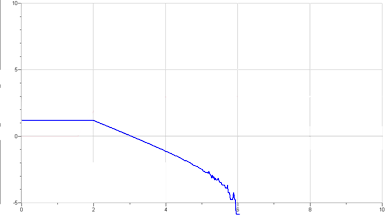
- Avec la résistance de 100 kohm, la pente de ln(V) (sur l’intervalle constant) vaut -1.1 et est égale à -c.
- Avec celle de 47 kohm la pente vaut -2.3, même constatation, est égale à -c (voir tableau).
- Ces observations sont parfaitement logiques compte tenu du fait que si l’on prend le logarithme de notre fonction d’ajustement, l’exponentielle se simplifie et il nous reste une fonction du premier degré dont la pente est égale à -c.
Extensions
– Quel pourcentage de la tension initiale reste-t-il après une constante de temps ? Et deux ? Et trois ?
- Nous avons obtenu les valeurs suivantes :
| 47 kohm | 100 kohm | ||||
| 0[s] | 3[v] | 100% | 0[s] | 2.85[V] | 100% |
| 0.47[s] | 1[v] | 30% | 1[s] | 0.916[V] | 33% |
| 0.94[s] | 0.33[v] | 11% | 2[s] | 0.286[V] | 10% |
| 1.51[s] | 0.1[v] | 3% | 3[s] | 0.076[V] | 3% |
- Après chaque constante de temps le potentiel a diminué de la même proportion (environ 70% de la valeur restante à chaque fois), on peut faire un parallèle avec les fonctions exponentielles du problème des bonbons qui ont le même comportement...la boucle est bouclée !
