Calcul de la masse d’un électron
par Antonin Urner, David Optyker, Théo Cormon
Lorsqu’une particule chargée pénètre dans une région de l’espace où règne un champ magnétique homogène (entre deux bobines plates par exemple) elle subit une force perpendiculaire à son vecteur vitesse et aux lignes de champ. La particule décrit alors une trajectoire circulaire dont le rayon dépend du champ magnétique, de la masse, de la charge et de la vitesse de la particule. Connaissant la tension qui a permis d’accélérer la particule et le courant qui circule dans les bobines, on peut trouver respectivement la vitesse de la particule et le champ magnétique dans lequel elle évolue. La mesure du rayon de sa trajectoire permet alors de déterminer le rapport e/m de sa charge à sa masse.
Procédure
Nous avons effectué 3 fois l’expérience en changeant a chaque fois la tension du canon à électrons. Durant chaque séance de mesure nous avons fait varier le courant qui parcourt les bobines d’Helmholtz de 0.8 (A) à 2.2 (A) . Nous avons par la suite reporté le diamètre du cercle décrit par les électrons pour chacun de ces I.
Tableau de données
Dans ce tableau nous avons reporté les rayons du cercle formé par la trajectoire des électrons, selon l’intensité du courant (bobines de Helmholtz) et la tension (canon à électron).
| 150(V) | 6.45 | 5.00 | 4.05 | 3.55 | 3.10 | 2.70 | 2.50 | 2.25 |
| 200(V) | 6.00 | 4.90 | 4.25 | 3.70 | 3.25 | 2.85 | 2.65 | |
| 250(V) | 6.50 | 5.60 | 4.75 | 4.25 | 3.70 | 3.30 | 3.00 |
Estimation du nombre de spires par bobine ainsi que la mesure du diamètre des bobines
| N=70 |
| D=0.3 (m) |
Analyse :
Pour calculer le quotient q/m nous avons besoin de plusieurs équations.
- La première consiste à égaler la force de Lorentz à la force centripète :
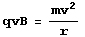
-
- Nous utilisons cette équation pour exprimer V
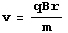
- Nous substituons ensuite V dans une seconde équation qui nous dit que le travail est égal à la variation d’énergie cinétique.
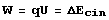
-
- Ce qui nous donne
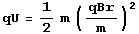
-
- D’où nous isolons le r
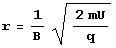
- Nous avons maintenant besoin de la troisième équation (celle du champ magnétique B entre les bobines de Helmholtz)
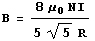
-
- Nous pouvons donc substituer B dans l’équation précédente
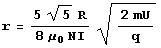
-
- Et comme r=k/I nous pouvons mettre l’équation sous cette forme
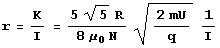
-
- D’où nous pouvons écrire que la pente vaut
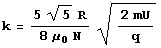
-
- Comme le K est connu, il suffit d’isoler le quotient q/m
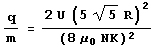
Graphique du rayon de la trajectoire décrite par les électrons en fonction de 1/I pour une tension de 150(V)
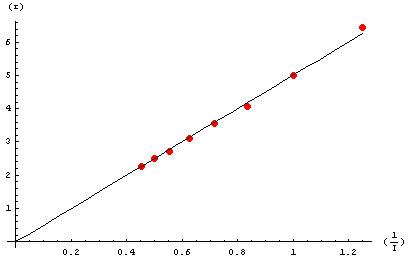
- Valeur de la pente :
- r = 5.01387*1/I
- Masse calculée de l’électron :
- m=2.36074*1031 (Kg)
Graphique du rayon de la trajectoire décrite par les électrons en fonction de 1/I pour une tension de 200(V)
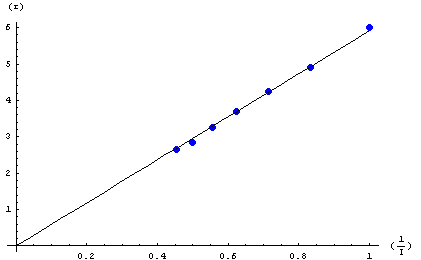
- Valeur de la pente :
r = 5.91177*1/I - Masse calculée de l’électron :
- m=2.46149*1031 (Kg)
Graphique du rayon de la trajectoire décrite par les électrons en fonction de 1/I pour une tension de 250(V)
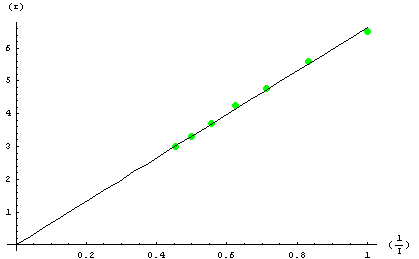
- Valeur de la pente :
r = 6.63139*1/I
- Masse calculée de l’électron :
- m=2.47778*1031 (Kg)
Comparaison avec les valeurs de la table numérique
La masse de l’électron étant de 9.1*10-31, nous constatons que nos valeurs sont quelque peu inférieures.
Calcul d’erreur
D’après les résultats obtenus, nous estimons l’incertitude sur la masse de l’électron à environ 75 %. Cela est dû à la grande imprécision des mesures du rayon de la trajectoire des électrons.
Conclusion
Cette expérience nous a permis de mieux comprendre le comportement des électrons dans un champ magnétique ainsi que de mettre en avant les relations entre ce comportement et des formules connues.
