Méthode : élaboration d’un graphique. Fiche élève.
par Maurice Dubath
Tableau des notions et des activités
Élaboration d’un graphique
1. Le choix des échelles se fait à partir des critères suivants : a) Plus le graphique est grand, meilleure est la précision. b) Les échelles doivent être simples (éviter une échelle qui demande un calcul pour placer chaque point).
2. Choisir la disposition de la feuille (verticale ou horizontale) qui permette les meilleures échelles.
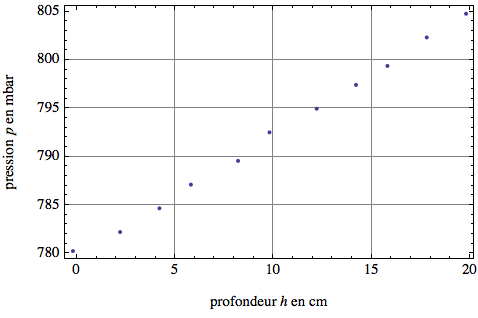
3. Placer les points (couples) en inscrivant une croix (x) sur le graphique.
4. L’origine, le couple (0 ;0), fait-il partie du graphique ? Si oui, il faut le placer sur celui-ci.
5. Ne jamais relier les points par des segments de droite.
6. Déterminer si les points sont répartis de façon régulière sur la feuille (alignés, formant une courbe etc.)
7. Tracer la droite (courbe) passant le plus près des points (répartir les écarts à la droite le mieux possible).
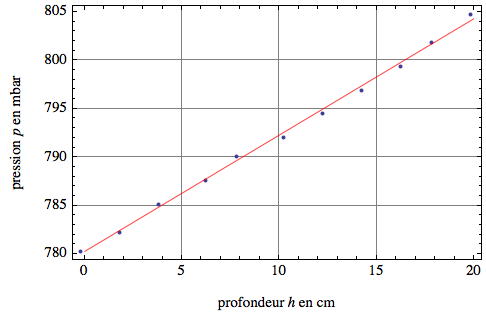
8. Les points du graphique, résultants d’une mesure, ne sont jamais parfaitement alignés (contrairement à une fonction mathématique). En revanche, il faut contrôler tout point qui serait éloigné de façon « anormale » de la droite ou de la courbe. Cette situation nous révèle souvent une mesure fausse ou une erreur de positionnement du point sur le graphique.
9. Si les points sont alignés, la droite tracée correspond à une relation ou fonction du premier degré (modèle mathématique) et elle peut être également exprimée sous forme algébrique :
y = ax + b
- x est la variable
- y est la fonction
- a est la pente de la droite et est constante
- b est l’ordonnée à l’origine
Si l’on connaît la fonction algébrique ci-dessus, on peut ensuite se passer du graphique pour les calculs (modèle). L’ordonnée à l’origine s’obtient par une lecture directe du graphique, mais la pente doit être calculée.
10. La pente est définie comme en mathématique (dénivellation/distance
horizontale) mais attention, il faut tenir compte des grandeurs représentées sur les axes et de leurs unités.
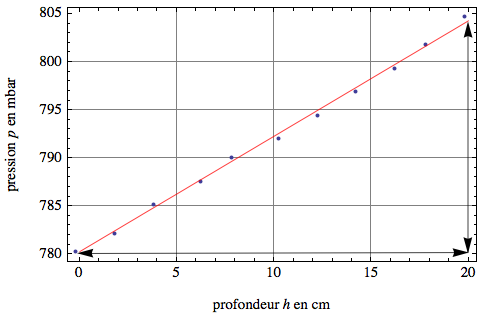
– Consignes :
- La pente se calcule à partir de la droite (on « oublie » les points).
- Le triangle qui permet le calcul de la pente doit être tracé sur le graphique.
- Le triangle doit être grand, si possible base et hauteur >10 cm (précision).
11. Rappel mathématique :
- La relation mathématique qui correspond à une droite qui passe par l’origine est une application linéaire.
- Si la droite ne passe pas par l’origine, c’est une application affine.
