Épreuve portant sur les expériences : loi d’Ohm, résistances en série et en parallèle, champ magnétique d’un solénoïde, e/m, force de Laplace, charge et décharge d’un condensateur.
– Champ : expériences de laboratoire
– Documents autorisés : Tables CRM, calculette.
– Lundi 2 avril 2007, CECNB, 8 h 05, salle 28, 160 min.
– Moyenne de classe : 4.44
– Écart type : 0.92
– Effectif : 17
Problème 1 (6 points)
Vous mesurez l’intensité du courant I qui traverse le filament d’une petite ampoule en fonction de la tension U à laquelle elle est soumise et vous obtenez les valeurs suivantes :
| U (V) | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I (A) | 0.00 | 0.21 | 0.36 | 0.47 | 0.56 | 0.62 | 0.68 | 0.72 | 0.78 | 0.80 | 0.83 |
- Établissez le graphique donnant $I$ en fonction de $U$.<(math>
- Calculez la résistance du filament lorsque
- Sachant que la température du filament vaut 20°C lorsque $U=U_{min}$ et 2500°C lorsque $U=U_{max}$, déterminez le coefficient de température $\alpha$ de la résistivité du filament.
Problème 2 (6 points)
- Exprimez la résistance équivalente de chacun des circuits ci-dessous.
- Calculez les valeurs de ces résistances équivalentes.
- Calculez l’incertitude sur chaque résistance équivalente si les valeurs des différentes résistances sont connues à 5%.

Données numériques : $R_1=$6 $\Omega$, $R_2=$14 $\Omega $, $R_3=$16 $\Omega $, $R_4=$20$\Omega $.
Problème 3 (6 points)
Vous mesurez le champ magnétique B au centre d’un solénoïde de 1 m de longueur en fonction du courant I qui le parcourt et vous obtenez les valeurs suivantes :
| I (A) | 0.0 | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 | 2.4 | 2.8 | 3.2 | 3.6 | 4.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| B (mT) | 0.07 | 1.18 | 1.83 | 2.94 | 3.94 | 5.08 | 5.97 | 6.91 | 8.18 | 9.04 | 10.10 |
- Exprimez le nombre de spires du solénoïde à partir de ces grandeurs.
- Calculez ce nombre de spires.
- Calculez l’incertitude affectant ce nombre pour une incertitude de 2 mm sur la longueur, de 0.1 A sur l’intensité du courant et de 0.01 mT sur le champ magnétique.
Problème 4 (6 points)
Vous mesurez la différence de potentiel entre les plaques d’un condensateur lorsqu’il se charge et lorsqu’il se décharge dans un circuit RC et vous obtenez les résultats suivants :
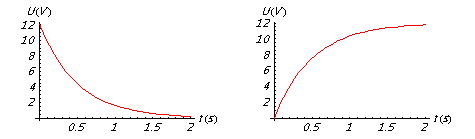
- Déterminez, à partir de ces mesures, la constante de temps $\tau$ associée à ce circuit.
- Donnez la signification physique de cette constante.
- Calculez la capacité du condensateur si la résistance vaut 500 $\Omega$.
Problème 5 (6 points)
Vous mesurez le rayon du cercle décrit dans un champ magnétique B=0.1 T par des particules accélérées. Vous reportez le rayon du cercle en fonction de $\sqrt U$ où $U$ est la tension d’accélération.
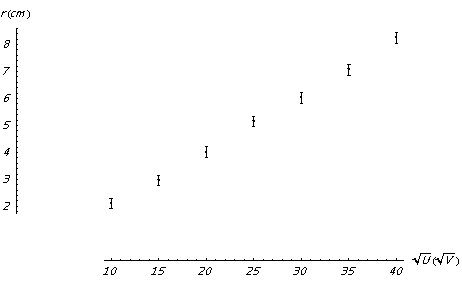
- Exprimez le rapport $\frac{q}{m}$ de ces particules à partir de ces grandeurs.
- Calculez ce rapport $\frac{q}{m}$ pour ces particules.
- Estimez l’incertitude affectant cette valeur.
Problème 6 (6 points)
Vous mesurez le courant nécessaire pour équilibrer une balance de Laplace en fonction de la distance d où se situe la petite masse mobile m=2 g et vous trouvez les valeurs suivantes :
| d (cm) | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 |
|---|---|---|---|---|---|---|---|---|---|
| I (A) | 0.00 | 0.04 | 0.06 | 0.10 | 0.14 | 0.17 | 0.21 | 0.24 | 0.27 |
- Exprimez à partir de ces grandeurs le champ magnétique B produit par l’aimant dans l’entrefer duquel se trouve une portion de longueur l.
- Calculez ce champ magnétique B à partir de ces mesures pour l=5 cm sachant que cette portion du conducteur se situe à une distance D=10 cm de l’axe de rotation de la balance.
- Estimez l’incertitude sur le champ magnétique B si l’incertitude sur d vaut de 1 mm, 5% sur D et 1% sur I.
– Barème
Corrigé
Problème 1
1. En reportant l’intensité du courant en fonction de la tension, on obtient un graphique qui a l’allure suivante :
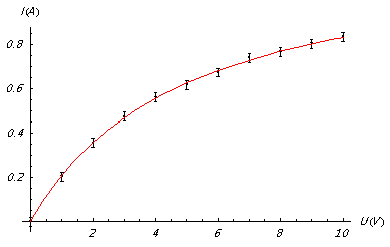
2. L’inverse de la pente $\frac{I}{U}$ en U=0 et en U=10 V donne la résistance.
– Rép. 4 Ω, 36 Ω.
3. En résolvant par rapport à $\alpha$ l’expression $\Delta R=R-R_0=\alpha R_0 \Delta T)$ donnant la variation de résistance $\Delta R$ en fonction de l’écart de température $\Delta T$ et en introduisant les résistances et les températures dans la solution, on obtient le coefficient $\alpha$ de température de la résistivité du filament.
– Rép. $3.23 \times 10^{-3}$ $K^{-1}$.
Problème 2
1. Pour le premier circuit (à gauche) nous calculons d’abord la résistance équivalente aux deux résistances $R_1$ et $R_2$ qui sont en série. Nous obtenons un circuit comportant deux résistances en parallèle $R_{12}$, $R_3$ dont la résistance équivalente $R$ fournit celle du circuit :
Pour le second circuit (à droite) nous calculons d’abord la résistance équivalente aux deux résistances $R_2$ et $R_3$ qui sont en série, puis aux deux résistances $R_{23}$, $R_4$ en parallèle. Nous obtenons un circuit comportant deux résistances en série $R_1$, $R_{234}$ dont la résistance équivalente $R$ fournit celle du circuit :
2. Le calcul donne les réponses suivantes :
– Rép. 8.89 ± 0.44 Ω, 18 ± 0.90 Ω.
3. L’incertitude sur la résistance équivalente $R$ peut se calculer ainsi :
– Rép 0.44 Ω, 0.90 Ω.
Problème 3
1. La pente du graphique donnant le champ magnétique au centre du solénoïde en fonction de l’intensité du courant qui le parcourt permet de trouver le nombre de spires :
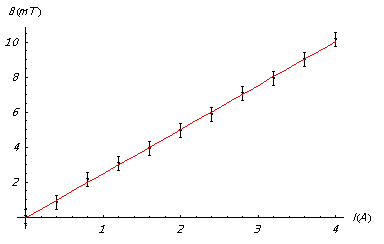
Le champ magnétique au centre d’un solénoïde est donné par :
La pente du graphique, qui est égale à $\frac{\mu_0 N}{l}$, permet d’exprimer le nombre de spires N :
2 Le calcul donne :
– Rép. 2002 ± 11.
3. L’incertitude sur le nombre de spires peut s’obtenir par :
– Rép. 11.
Problème 4
1. La loi de décharge du condensateur est donnée par :
En reportant ln(U) en fonction du temps, on trouve une droite de pente $-\frac{1}{\tau.}$
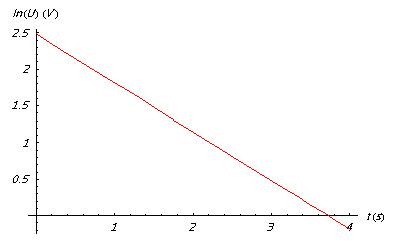
– Rép. 0.55 s.
2. La constante de temps $\tau$ correspond au temps après lequel la tension vaut $\frac{U_0}{e}$ lors de la décharge et à $U_0(1 - \frac{1}{e})$ lors de la charge du condensateur. Après un temps $\tau$, la tension aux bornes du condensateur vaut donc grosso modo 63% de la tension du générateur lorsqu’il se charge et 37 % de sa tension initiale lorsqu’il se décharge.
3. La constante de temps $\tau$ est égale à RC où R est la résistance du circuit et C la capacité du condensateur, donc :
– Rép. 1 mF.
Problème 5
1. Les particules décrivent un cercle. Elles sont donc soumises à une force centripète. D’autre part elles se déplacent dans un champ magnétique et subissent de ce fait la force de Lorentz. Égalons la force centripète à la force de Lorentz :
Utilisons le théorème de l’énergie cinétique pour exprimer la relation entre la tension d’accélération U et la vitesse acquise :
En substituant la vitesse obtenue à partir du théorème de l’énergie cinétique dans l’expression de l’égalité des forces centripète et de Lorentz, nous obtenons :
En reportant r en fonction de $\sqrt U$, on obtient donc une droite dont la pente permet de trouver le rapport charge sur masse de la particule :
2. Le calcul, avec une pente estimée à 0.002 unités SI, donne :
– Rép. $5\times 10^7$ $\frac{C}{kg}$
3. L’incertitude sur le quotient $Q=\frac{q}{m}$ s’obtient par :
Pour une incertitude relative de 10 % sur le champ B et sur la pente, on trouve :
– Rép. $2 \times 10^5$ $\frac{C}{kg}$
1. La balance est en équilibre lorsque le moment de la force de Laplace est égal en grandeur au moment de la force pesante :
En reportant le courant nécessaire pour équilibrer une balance de Laplace en fonction de la position du contrepoids, on obtient une droite :
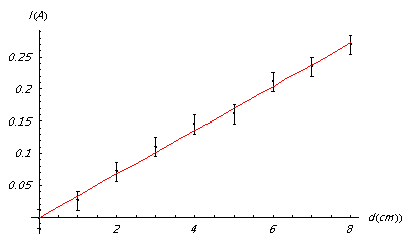
L’équation de cette droite est donnée par :
La pente qui est égale à $\frac{mg}{lBD}$ permet d’exprimer le champ magnétique B :
2. Le calcul donne, pour une pente estimée à 3.4 A/m :
– Rép. 1.15 ± 0.08 T
3. L’incertitude sur B s’obtient à l’aide de :
– Rép. 0.08 T
Répartition des points par question
| Question 1 | Question 2 | Question 3 | Total | |
|---|---|---|---|---|
| Problème 1 | ||||
| Problème 2 | ||||
| Problème 3 | ||||
| Problème 4 | ||||
| Problème 5 | ||||
| Problème 6 | ||||
| Total des points |
