Étude de la chute de deux corps de masses différentes depuis la tour de Pise.
Le but de cet article est d’étudier la chute de deux corps ayant des caractéristiques différentes l’une de l’autre en s’aidant du logiciel STELLA.
Introduction
Cette expérience consiste à lâcher, depuis le sommet de la tour de Pise, deux billes ayant des caractéristiques différentes.

La tour de Pise, construite entre 1173 et 1350, soit une durée de 177 ans, est haute 54.5 mètres. Cette tour a commencé à pencher vers 1274 lors de la construction du 3ème étage (elle en conte 8 aujourd’hui). C’est pour cela qu’aujourd’hui on l’appelle la tour penchée. La tour est actuellement inclinée d’un angle de 5,5°, ce qui fait que le dernier étage est décalé de 5.2 mètres par rapport à la base de la tour.
Notions physiques
La chute d’un objet depuis une certaine hauteur dépend de certaines forces. Dans notre cas il y en a trois :
- Il y a tout d’abord le poids, appelé aussi force de pesanteur. Cette force est toujours dirigée vers le bas. Elle est proportionnelle à la masse m de l’objet lâché et à l’attraction terrestre g.
$ P = mg $ - Ensuite il y a la force de frottement. Cette force est toujours opposé au mouvement de la bille. Elle est proportionnelle à la masse volumique de l’air ρ, à la section apparente S de la bille, définie par son rayon r, au coefficient de pénétration dans l’air Cx et à la vitesse v de la bille au carré.
$ F_{frott}\ = \frac {1} {2} \rho \ S \ C_{x} \ v^2 $ - Et pour finir la force d’Archimède. Tout corps plongé dans un fluide (liquide ou gazeux), subit une force verticale, dirigée de bas en haut. Cette force est appelée aussi poussée d’Archimède. Cette force est proportionnelle à la masse volumique du fluide ρ dans lequel se trouve l’objet, dans ce cas de l’air, à l’attraction terrestre g et au volume V de l’objet.
$ F_{archi}\ = \rho \ g \ V_{imergé} $
Grâce à ces trois forces, il nous est désormais possible de calculer l’accélération d’un objet en chute. En effet, l’accélération est égale à la somme des forces divisée par la masse de l’objet en chute libre :
$ a\ = \frac{\Sigma \vec F}{m}$
Voici la formule de l’accélérarion pour cette expérience :
$ a\ = \ \frac {(-P+F_{frott}+F_{archi})} {m} $
Logiciel STELLA
A quoi sert le logiciel STELLA ?
STELLA est un intégrateur numérique permettant d’étudier des cas concrets et de les étudier à l’aide de graphiques.
Pour réussir à étudier cette expérience il faut tout d’abord créer un modèle avec STELLA dans le but de simuler la chute des deux billes. Voici le modèle STELLA qui permet d’étudier ce problème.
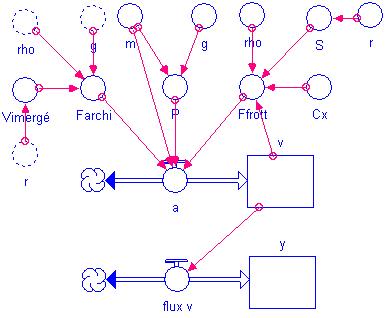
Quand la modélisation est terminée, il faut entrer les données dans STELLA pour qu’il puisse effectuer les différents calculs d’intégration. Voici les données qui permettent de simuler l’expérience du modèle STELLA qui ce trouve ci-dessus :
| Elements | Descriptif | Contenu/Valeur | Unités |
|---|---|---|---|
| y | Hauteur de la tour de Pise | 54.5 | m |
| v | Vitesse initiale de la bille | 0 | m/s |
| flux v | Vitesse de la bille | v | m/s |
| a | Accélération | (-P+Ffrott+Farchi)/m | m/s2 |
| P | Poids de la bille | m*g | N |
| Ffrott | Force de frottement | 0.5*rho*Cx*S*v^2 | N |
| Farchi | Force d’Archimède | g*rho*Vimergé | N |
| g | Attraction terrestre | 9.81 | N/kg |
| Cx | Coefficiant de pénétration dans l’air | 0.24 | |
| rho | Masse volumique de l’air | 1.293 | kg/m3 |
| S | Séction apparente de la bille | PI*r^2 | m2 |
| Vimergé | Volume de la bille | 4/3*PI*r^3 | m3 |
A noter qu’il manque deux données (m et r) dans ce tableau tout simplement parce qu’elles seront données dans les différents cas qui suivent.
Pour étudier la chute des deux billes dans cette expérience, nous allons analyser deux différents cas. Nous allons aussi étudier les différences entre la chute de ces deux objet.
Cas 1
Premièrement, nous allons voir ce qui se passe lorsqu’on lâche deux billes de mêmes tailles, ayant donc le même rayon, mais étant de poids différents.
Voici les données manquantes qui complètent le tableau ce trouvant ci-dessus :
| Eléments | Descriptif | Valeur bille 1 | Valeur bille 2 | Unités |
|---|---|---|---|---|
| r | Rayon de la bille | 0.15 | 0.15 | m |
| m | Masse de la bille | 0.5 | 1 | kg |
Voici le graphique de la position qu’on obtient pour la bille 1 et la bille 2 :
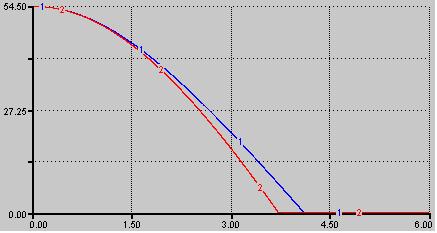
La première constatation qu’il est possible de faire après avoir vu ce graphique est que la bille 1, plus légère, met plus de temps à toucher le sol que la bille 2.
La bille 2 touche le sol après 3.7 secondes. La bille 1 arrive 4 dixièmes après, c’est-à-dire qu’elle met 4.1 secondes pour effectuer le trajet sommet-sol.
De plus lorsque la bille 2 touche le sol, la bille 1 est encore en l’air. On peut voir sur le graphique qu’elle se trouve à une hauteur 7.73 mètres.
On peut en conclure donc que plus un objet que l’on lâche depuis une certaine hauteur est léger, plus cet objet mettra du temps à toucher le sol.
Ce problème peut aussi être démontré sans l’aide de STELLA, mais en calculant l’accéleration des deux billes. Voici les valeurs de l’accélération initiale des deux billes :
– abille 1=-9.45 m/s2
– abille 2=-9.63 m/s2
Il faut noter que les valeurs sont négatives car l’accélération des deux billes est dirigée vers le bas.
Si on prend la valeur absolue de ces deux valeurs, on peut constater que l’accélération de la bille 2 est plus grande que l’accélération de la bille 1. Avant même de lancer la simulation, on peut en déduire de ces valeurs que la bille 2 arrivera avant la bille 1.
Cas 2
Dans ce deuxième cas, nous allons voir ce qui se passe lorsqu’on lâche deux billes de même poids mais de tailles différentes, c’est-à-dire n’ayant pas le même rayon.
Voici les données manquantes :
| Eléments | Descriptif | Valeur bille 1 | Valeur bille 2 | Unités |
|---|---|---|---|---|
| r | Rayon de la bille | 0.15 | 0.30 | m |
| m | Masse de la bille | 1 | 1 | kg |
Voici le graphique de la position qu’on obtient pour la bille 1 et la bille 2 :
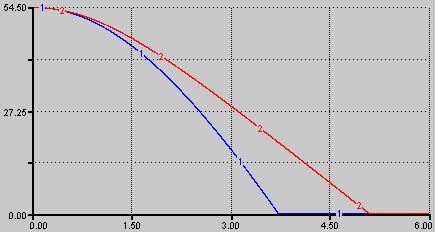
Cette fois-ci, on peut constater que c’est la bille 2, plus grande, qui met plus de temps à atteindre le sol que la bille 1.
La bille 1 touche le sol après 3.7 secondes. La bille 2 arrive 1.35 secondes après, c’est-à-dire qu’elle met 5.05 secondes pour effectuer le trajet sommet-sol.
De plus lorsque la bille 1 touche le sol, la bille 2 est encore en l’air. On peut voir sur le graphique qu’elle se trouve à une hauteur de 19 mètres.
On peut en conclure donc que plus un objet qu’on lâche depuis une certaine hauteur est grand, c’est-à-dire qu’il a un plus grand rayon, plus cet objet mettra du temps à toucher le sol.
Comme dans le cas 1, STELLA n’est pas indispensable, il est possible de prevoir ce qui va se passer uniquement en calculant l’accélération initiale des deux billes. Voici les résultats de ces calculs :
– abille 1=-9.63 m/s2
– abille 2=-8.37 m/s2
Là aussi, les valeurs sont négatives car l’accélération des deux billes est dirigée vers le bas.
Si on prend la valeur absolue de ces deux valeurs, on peut voir que l’accélération de la bille 1 est plus grande que l’accélération de la bille 2. Avant même de lancer la simulation, on peut constater que la bille 1 arrivera avant la bille 2.
Conclusion
Il est possible de vérifier avec cette expérience que la chute d’un objet dépend de plusieurs facteurs. Il y a tout d’abord les forces qui se comptent au nombre de trois (poids, force de frottement et force d’Archimède). Et puis il y a les caractéristiques mêmes de l’objet étudié, à savoir sa masse, son rayon, etc. L’étude de ce type d’expérience sans le logiciel STELLA peut s’avérer complexe et parfois fastidieuse à cause des nombreux calculs compliqués. STELLA est un outil intéressant qui facilite vraiment les choses et en plus nous propose une nouvelle approche des sciences (en particulier math et physique).
