Différentes mesures de la force de Laplace, qui permettront de calculer la valeur du champ magnétique.
Dans ce travail, nous allons mesurer la force agissant sur un conducteur placé dans un champ magnétique et parcouru par un courant. En reportant les données dans un graphique, nous pourrons déterminer la fonction de cette force et en déduire les composantes, dont la valeur du champ magnétique.
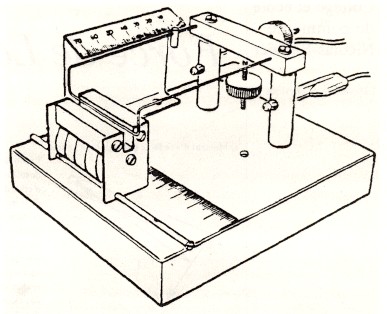
La longueur utile l du conducteur placé dans l’entrefer du bloc aimanté est de 5cm. Elle subit la force de Laplace (dirigée vers le haut) lorsque le conducteur est parcouru par le courant I. Cette force de Laplace produit un moment M1 = Fl d1 avec d1 = 10cm qui est la distance qui sépare la portion utile du conducteur des deux pivots (qui jouent le rôle d’axe de rotation). On équilibre ce moment M1 en produisant un moment opposé, c’est à dire en déplaçant une masse de m = 1.8g le long du conducteur support qui est parallèle à une échelle graduée. Le curseur produit un moment M2 = mgd2. On a donc à l’équilibre Fl d1 = mg d2.
– Tableau de mesures
| mesures | distance d2 [m] | Intensité [A] | F l [N] |
|---|---|---|---|
| 1 | 0.01 | 0.25 | 1.766*10-3 |
| 2 | 0.02 | 0.6 | 3.53*10-3 |
| 3 | 0.03 | 0.9 | 5.29*10-3 |
| 4 | 0.04 | 1.2 | 7.06*10-3 |
| 5 | 0.05 | 1.5 | 8.83*10-3 |
| 6 | 0.06 | 1.8 | 1.059*10-2 |
| 7 | 0.07 | 2.1 | 1.236*10-2 |
Autres données :
masse = 1.8 [g] ; g = 9.81 [m/s2] ; d1 = 0.1 [m] ; l = 0.05 [m]
– Pour calculer la force de Laplace :
Moment de force 1 = Moment de force 2
Force de Laplace x d1 = m x g x d2
Force de Laplace = (m x g x d2)/ d1
– Représentez sur un graphique, f en fonction de i et, à partir de la droite f = k i (avec k = l B), calculez la valeur du champ magnétique B
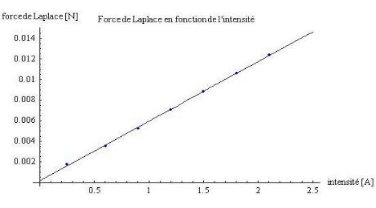
La droite obtenue par un "fit" dans mathematica, nous donne
f (i) = 0.000166528 + 0.00577968 i
Nous savons que f = k i et k = l B.
Donc, B = k / l.
B = (0.000166528 + 0.00577968) / 0.05 = 0.1189 ± 1.19*10-4 [tesla]
– Remarque sur les incertitudes : on ne sait pas exactement où s’arrête le champ B à l’extérieur de l’aimant. On prend comme longueur utile du conducteur 0.05 +/- 0.02 [m]. Effectuez le calcul d’incertitude sur B.
Pour faire le calcul d’incertitude complet sur B (le delta de B), il faudrait remonter jusqu’au début des procédure. Pour trouver B, nous avons eu besoin de m, g, d2, d1, I et l. Nous n’avons pas l’erreur absolue de chaque mesure, donc effectuons uniquement la dernière partie : B = k / l
Formule de calcul d’incertitude (erreur absolue)
X = A / B : deltaX = (A * deltaB + B * deltaA)/B2
Admettons donc qu’il n’y ait pas d’imprécision sur k (ce qui est en réalité faux, vu le nombre de paramètres utilisés pour trouver k).
delta B = k * delta l + l * delta k
delta B = (0.000166528 + 0.00577968) * 0.02 = 1.19*10-4 [tesla]
