
Examen du « paradoxe » des jumeaux, dont l’un, Bernard, voyageant dans l’espace interplanétaire vieillit moins vite que son frère Alain resté sur terre.
par bernard.vuilleumier
Le « paradoxe » des jumeaux dont l’un, Bernard, voyageant dans l’espace interplanétaire vieillirait moins vite que son frère Alain resté sur terre, a inspiré toute une littérature qui n’a pas toujours bien mis en évidence le véritable paradoxe.
Le « paradoxe » des jumeaux dont l’un, Bernard, voyageant dans l’espace interplanétaire vieillirait moins vite que son frère Alain resté sur terre, a inspiré toute une littérature qui n’a pas toujours bien mis en évidence le véritable paradoxe. Cette question stimule aujourd’hui encore des discussions entre les spécialistes de la relativité. Ils semblent s’accorder sur deux points : 1° le paradoxe ne réside pas dans le fait que le temps s’écoule différemment pour les deux jumeaux ; 2° le paradoxe ne ressortit pas strictement à la relativité restreinte qui ne sait relier la description d’événements que pour des observateurs animés d’un mouvement relatif rectiligne et uniforme. Or le paradoxe des jumeaux fait intervenir des comparaisons dans le même système final et doit, pour cela, introduire une accélération pour un des deux systèmes.
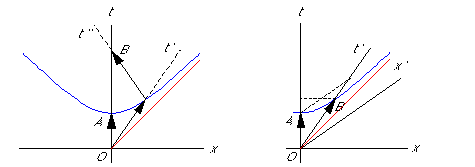
A gauche : Diagramme d’espace-temps. En reliant O à un événement quelconque de l’hyperbole on obtient un intervalle unité. La durée écoulée se mesure sur les lignes d’univers t pour A, t’ et t’’ pour B. Cette mesure doit se faire sur chaque ligne d’univers avec l’unité qui lui est associée. Le temps écoulé pour le voyageur B vaut 2 unités alors qu’il est supérieur à 2 unités pour le sédentaire A.
A droite : En relativité restreinte le temps n’est plus universel et il s’écoule différemment selon la vitesse relative de translation rectiligne uniforme des référentiels. Mais les effets sont réciproques : l’unité de temps d’un système projetée dans un autre système paraît dilatée quel que soit le système de départ.
La pierre angulaire de la relativité restreinte est la réciprocité des conclusions auxquelles arrivent les observateurs. L’unité de temps de B projetée sur la ligne d’univers t paraît dilatée à A. Mais l’unité de temps de A projetée sur la ligne d’univers t’ de B paraît aussi dilatée à B. Si les jumeaux n’ont pas le même âge lorsqu’ils se retrouvent, il n’y a plus réciprocité. C’est dans cette rupture de réciprocité des conclusions que réside le paradoxe. La relativité restreinte est-elle à revoir pour autant ? Comment lever ce paradoxe ?
Le paradoxe des jumeaux
Le jour de ses vingt et un ans, Bernard quitte son frère jumeau Alain qui reste sur Terre et s’en va le long de l’axe des x à une vitesse égale aux 24/25 de celle de la lumière. Il voyage pendant sept ans, tels qu’il les mesure dans son référentiel puis il fait demi-tour et met encore sept années de son temps pour revenir à la même vitesse.
– a) Quel est l’âge de Bernard à son retour ?
– b) Tracez le diagramme d’espace-temps qui montre le mouvement de Bernard. Vous indiquerez les coordonnées x et t du point de retour et du point où il retrouve son frère. Vous admettrez pour simplifier que la Terre constitue un système de référence inertiel et vous prendrez l’événement constitué par le départ de Bernard comme origine.
– c) Quel est l’âge d’Alain au moment où Bernard est de retour ?
Réponses dans le cadre de la relativité restreinte
– a) Bernard voyage pendant 14 ans. Il a donc 21+14=35 ans à son retour.
– b) Diagramme d’espace-temps des jumeaux :
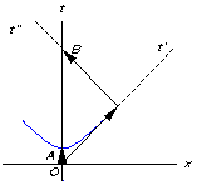
– c) Le temps de voyage de Bernard projeté sur la ligne d’univers d’Alain paraît dilaté et vaut :
Au retour de Bernard, Alain aura donc 21+50=71 ans.
D’où provient le paradoxe ?
Le « paradoxe » réside dans le fait qu’il n’y a plus réciprocité entre les observations faites par A et celles faites par B. Mais il y a un usage illégitime de la transformation de Lorentz pour calculer le temps écoulé pour A durant le voyage de B. En toute rigueur, cette transformation ne doit s’utiliser que pour relier des observations d’événements faites depuis des systèmes de référence en translation rectiligne uniforme les uns par rapport aux autres. Or le référentiel de B n’appartient pas à cette catégorie de référentiels car il subit une accélération au point de rebroussement.
Sources. Pour en savoir plus.
• M.-A. Tonnelat, Histoire du principe de relativité, Flammarion 1971.
• Taylor et Wheeler, A la découverte de l’espace-temps, Dunod,1970.
• Article « Paradoxe des jumeaux » de wikipedia
• Discussions à propos du paradoxe sur wikipedia
