Travail à rendre d’applications des maths.
Le chaos est parmi les plus jeunes sciences. Ces origines sont obscures mais nous pouvons approximer sa découverte au environ des années 70, elle est depuis considéré par certains comme étant la plus fascinante des sciences. Une des particularité du chaos, c’est que l’on peut en parler dans différent domaines, c’est une science mais on peut également l’a décrire comme une phénomène de la vie de tout les jours. Ce travail a donc pour but de présenter le chaos en science mais aussi en général.
Le Chaos en science
On défini un phénomène chaotique comme étant un phénomène déterministe qui n’est pas périodique et qui se caractérise par une hypersensibilité aux conditions initiales. C’est cette sensibilité qui fait que le phénomène est si imprévisible.
Théoriquement, on peut prévoir très précisément l’évolution de tels systèmes. Dans la pratique (exemple avec sa découverte), étant donné que la mesure des conditions initiales nécessite une précision extrême, il est impossible de créer le chaos que l’on désire. On comprend alors la difficulté qu’ont les expérimentateurs à prévoir l’évolution d’un système chaotique, étant donné que la précision des mesures ne peut en pratique pas être suffisante pour connaître les conditions initiales de manière satisfaisante.
On peut illustrer la sensibilité du chaos aux conditions initiales par l’effet papillon. Cet effet papillon consiste en l’image suivante. On peut considérer que le simple battement d’aile d’un papillon en Australie peut entraîner une tempête sur la côte américaine.
Cela signifie qu’une erreur de mesure en apparence mineure a de grandes répercussions quant à l’évolution des systèmes chaotiques.
La différence entre chaos et phénomènes aléatoires
Il est important de différencier le chaos d’un phénomène aléatoire. En effet, on peut intuitivement avoir tendance à considérer qu’un phénomène qui n’est pas prévisible est chaotique. Non ! Un exemple comme celui du mouvement Brownien le démontre. Ce mouvement n’est pas chaotique mais aléatoire, c’est-à-dire qu’il est régi par une loi probabiliste.
Quant au phénomène chaotique qui est décrit de manière déterministe, c’est-à-dire avec des outils mathématiques qui devrait permettre une approche précise et a priori certaine. On constate même qu’il n’y a rien qui lie le chaos et l’aléatoire puisque même une approche probabiliste de l’évolution d’un système chaotique n’aboutirait à rien.
Quelques exemples
Phénomènes chaotiques
– Phénomènes météorologiques
Un cyclone est un phénomène météorologique qui se caractérise par de forts vents et de fortes pluies. Les météorologues connaissant ses conditions de formation, on pourrait penser qu’ils sont en mesure d’expliquer le phénomène de manière précise : prévoir sa trajectoire, son évolution, au moins à court terme. Pourtant, ils se trouvent incapables de faire toute prévision en pratique.
– Le ballon de baudruche
Un ballon de baudruche gonflé qu’on lâche (sans vitesse initiale), dans une direction déterminée, se dégonfle et suit dans l’air une trajectoire sans régularité aucune.
Quand on répète l’expérience dans des conditions initiales aussi semblables que possible, (position, direction, volume du ballon, absence de vitesse initiale…), on constate que le ballon suit à nouveau une trajectoire sans régularité, mais de plus que celle-ci est totalement différente de celle obtenue lors du premier lâcher, contrairement à ce à quoi on aurait pu s’attendre. C’est cette totale imprévisibilité qui donne à penser que ce mouvement est chaotique.

– Une population d’insecte
Cette exemple sera une étude d’un point de vue théorique de l’évolution d’une population d’insectes. Elle sera illustré à l’aide de Mathematica.
Nous nous basons sur deux hypothèses :
- Les insectes pondent leurs oeufs, en hiver ces insectes meurent et au printemps les oeufs éclosent.
- Pour se simplifier la vie, on normalise la population à 1 (100%). Le taux de reproduction est désigné par r. La population est désignée par x.
Nous avons une évolution "discrète" en raison de l’hypothèse 1 (on décrit l’évolution d’année en année).
Si un insecte pond deux oeufs par année et qu’on part d’une population initiale de deux insectes, on aura l’année suivante 4 insectes.
Ce comportement n’est pas réaliste. Il faut trouver un moyen de limiter la croissance. Il suffit de faire en sorte que lorsque la population approche de la valeur maximale (1), la croissance diminue et s’annule lorsque x=1. On écrira donc
On récris notre NestList.
Il faut faire un Table pour varier les taux de reproductions.
Finalement, on fait varier la NestList avec Nest.
En représentant tout ça sur un seul graphique nous donnera le graphique ci-dessous. C’est un phénomène chaotique.
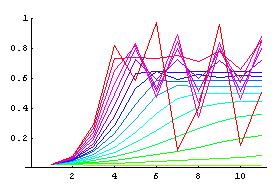
Phénomène aléatoire
– Le mouvement Brownien
Ce mouvement peut être illustré par un grain de poussière contenu dans de l’eau et observé au microscope. On voit que le grain de poussière est soumis à un bombardement incessant par les molécules d’eau dû à l’agitation thermique. Si un grand nombre de molécules frappent en même temps la particule d’un même côté, elles peuvent déplacer celle-ci de façon notable. Cependant les mouvements des particules en suspension sont indépendants les uns des autres, même lorsque les particules sont séparées par une distance inférieure à leur propre diamètre. Le mouvement brownien est un phénomène doublement aléatoire : la trajectoire du grain de poussière est rendue aléatoire par les fluctuations aléatoires des vitesses des molécules. De plus, la résolution du microscope ne permet pas d’entrevoir la réelle complexité de la trajectoire.
On ne peut donc prévoir la trajectoire précise du grain de poussière car les molécules d’eau ainsi que leurs interactions sont innombrables. Le fait que le déplacement soit imprévisible n’est pas dû à une éventuelle évolution chaotique du système, mais à un la présence de phénomènes aléatoires.
Le jeu du chaos
Ce "jeu" va nous permettre de découvrir les notions d’attracteur et de figure fractale. Pour commencer, il vous faut une feuille de papier, un crayon, un compas, une règle et un dé. Dessinez un triangle équilatéral sur la feuille de papier et numérotez les sommets de 1 à 3. Choisissez arbitrairement un point $P_0$ sur votre feuille. Tirez au hasard, à l’aide du dé, un des sommets du triangle. Reliez $P_0$ à ce sommet et placez, au milieu du segment ainsi obtenu, le point $P_1$. Tirez au hasard un des sommets du triangle. Reliez $P_1$ à ce sommet et placez, au milieu du segment ainsi obtenu, le point $P_2$, et ainsi de suite. Nous ferons tout cela avec l’aide de Mathematica.
Commençons pas dessiner notre triangle.
Il nous faut maintenant des fonctions qui permettent d’obtenir le milieu du segment qui relie un point p à un des trois sommets.
Occupons nous du dé à 3 faces maintenant. Ce dé doit être capable de tirer au hasard une des trois fonctions lors de chaque jeter. Nous mettons les trois fonctions en liste. La notation ci-dessous permet d’extraire un élément de la liste.
Pour appliquer le résultat de notre tirage à un point, nous définissons une fonction.
Nous souhaitons évaluer cette fonction on partant d’un point initial tiré au hasard, puis une fois le résultat obtenu, répéter l’opération en prenant comme point initial le dernier obtenu.
Il nous reste plus qu’à "ListPloter" !
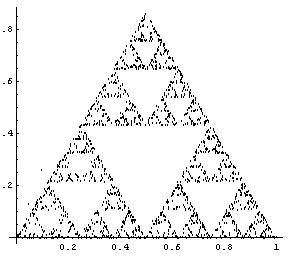
La répartition des points est prévisible, elle converge vers un attracteur. En revanche, l’itinéraire obtenu en reliant les points successifs en revanche est totalement imprévisible, ce qui signifie que l’on ne peut pas prévoir à l’avance où se situera tel ou tel point, bien que la répartition globale des points soit parfaitement connue !
Conclusion
Le chaos est une notion qui depuis sont avènement (tout comme la relativité) à chambouler bien des idées. Il est vrai que c’est un sujet très vaste et qu’on peut facilement s’y perdre. C’est également une science qui a été découverte récemment, il y a encore sûrement quelques ambiguïtés. Mais qui sait, il y aura peut-être bientôt une nouvelle notion qui arrivera et qui à nouveau chamboulera tout.
Source & référence utilisées
owl-spip L’article sur le Jeu du chaos.
Tpe Chaos Ifrance tout le site.
site de Julien Salort dans la rubrique Chaos.
