Analyse du mouvement harmonique simple d’un poids.
par Aymeric Genet, Caroline Calpini
Ceci est un rapport de laboratoire d’une analyse du mouvement harmonique simple d’une masse accrochée à un ressort. L’intention était de comprendre ce mouvement et de comparer nos résultats aux formules mathématiques. Nos résultats et graphiques y sont compris.
Le mouvement harmonique simple concerne un ensemble d’objets pouvant osciller ou vibrer. Il y a deux sortes de vibrations : les vibrations mécaniques, un ressort par exemple, ou bien des vibrations électriques, comme un signal radio. On l’appelle mouvement harmonique simple, à cause de la proportionnalité entre l’étirement, la compression et la force de rappel exercée par le ressort.
Pour expérimenter, prenons juste : une masse accrochée à un ressort.
Le modèle mathématique de ce mouvement peut modéliser la position de la masse par l’équation :
| Terme | Définition |
|---|---|
| y | Déplacement à partir de la position d’origine y0 |
| A | Amplitude du mouvement |
| f | Fréquence de l’oscillation |
| t | Temps |
| Φ | Constante de phase |
L’expérience a pour but d’éclaircir les termes de l’équation.
Objectifs
- Mesurer la position et la vitesse en fonction du temps pour une masse suspendue à un ressort.
- Comparer le mouvement observé au modèle mathématique du mouvement harmonique simple.
- Déterminer l’amplitude, la période, et la constante de phase du mouvement harmonique.
Tableau des données
| Essai | Masse (g) | y0 (cm) | A (cm) | T (s) | f (Hz) |
| 1 | 60 | 0.7 | 5 | 0.8 | 1.25 |
| 2 | 60 | 0.7 | 8 | 0.8 | 1.25 |
| 3 | 110 | 0.6 | 10 | 1.1 | 0.9 |
Analyse
1. Comparez les diagrammes du mouvement et de la vitesse. En quoi se ressemblent-ils ?
L’aspect de ces deux diagrammes se ressemble, car ce sont tous les deux des sinusoïdes, mais seules l’amplitude et la phase diffèrent, comme nous le montre le graphique.
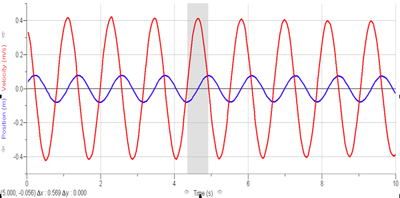
2. Où est la masse quand la vitesse est zéro ? Où est la masse quand la vitesse est maximale ?
Quand la vitesse est zéro, la position de la masse est au minimum ou au maximum.
Quand la vitesse est maximale, la position de la masse se retrouve à la position du y0.
Le graphique nous démontre clairement nos réponses : lorsque la vitesse est nulle la position est extrémale et lorsque la vitesse est maximale la position correspond à la position d’équilibre.
3. Est-ce que la fréquence f semble dépendre de l’amplitude du mouvement ? A-t-elle beaucoup varié au cours de vos tests ?
La fréquence f n’a pas vraiment varié au cours de nos tests. Nous n’avons pas assez de données exactes pour en tirer une conclusion définitive, mais nos essais nous permettent de savoir que si l’amplitude A change, ni la fréquence f ni la période T ne changent. Les formules-même de la fréquence f et de la période T vérifient notre remarque.
Équation de la période T : $T = 2 \pi \sqrt{ \frac{m}{k} }$
On remarque que dans les deux formules, l’amplitude ne fait pas son apparition. Donc nous en concluons que la fréquence f ne varie pas suivant l’amplitude A.
4. Est-ce que la fréquence f semble dépendre de la masse ? A-t-elle beaucoup varié au cours de vos tests ?
Oui elle dépend de la masse, même si dans nos résultats obtenus, la fréquence ne change pas beaucoup. Les formules-même de la fréquence f et de la période T vérifient notre remarque.
Équation de la période T : $T = 2 \pi \sqrt{ \frac{m}{k} }$
On remarque que dans l’équation de la période T, la masse m fait son apparition. Donc la fréquence f contenant cette équation de la période T se voit modifiée si la masse m varie.
Graphiques
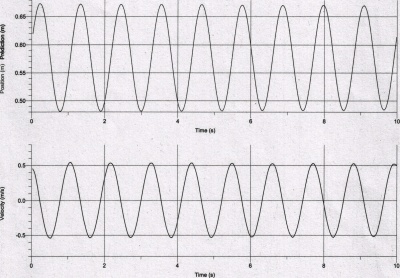
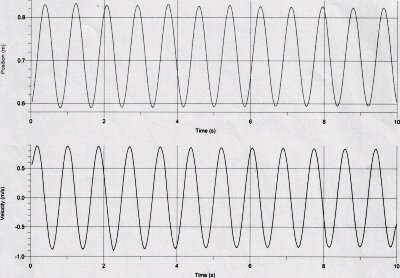
Conclusion
À l’aide de moyens informatiques, nous avons pu mesurer la vitesse et la position d’une masse oscillante et vibrante par rapport au temps. Grâce à cela, nous avons pu observer le mouvement pour l’analyser et obtenir des résultats que l’on a par la suite comparés et vérifiés avec les formules mathématiques, ce qui nous a donné une nouvelle image de la physique.
