Modèles d’oscillateur harmonique non forcé et forcé sur Stella.
par Diego Gonzalez-Candia
On peut trouver le phénomène d’oscillations dans de nombreuses applications physiques, comme par exemple, les oscillations d’un pendule ou encore le mouvement produit par le vent sur un pont suspendu et même dans l’électricité.
Je vais d’abord réaliser le modèle d’un oscillateur harmonique (non forcé) sur Stella, pour ainsi meiux comprendre par la suite l’oscillateur harmonique forcé.
Oscillateur harmonique
Prenons comme exemple un système masse-ressort :
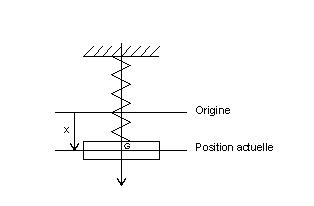
Il faut que la position d’équilibre de la masse coïncide avec l’origine de l’axe x pour que la force de rappel puisse s’exprimer, si l’on néglige la force de frottement, par :
$ F rappel = -kx $
Pour obtenir l’accélération on fait appel à relation fondamentale de la dynamique qui dit que l’accélération est égale à la somme de toutes le forces divisées par la masse.
« k » correspond à la raideur du ressort et « x » représente l’élongation du ressort, la force de rappel est négative car elle est toujours opposée à « x ».
Pour simuler ce système dans Stella il faut le construire de cette manière :

Et voici les données introduites :
Résultat graphique de la position en fonction du temps :

Oscillateur harmonique avec frottement
On peut aussi simuler un oscillateur harmonique en prenant en compte cette fois la force de frottement, dont voici le modèle :

Voici les données introduites :
Résultat graphique de la position en fonction du temps :

Contrairement au dernier résultat, ici on remarque que la masse va finir par s’arrêter au fil du temps, ceci est dû au frottement.
Oscillateur harmonique forcé
A présent je vais réaliser le modèle de l’oscillateur harmonique forcé. Cette fois une force d’excitation intervient. Cette force est définie par une amplitude et une vitesse angulaire qui dépend d’une fréquence. Si la fréquence de l’excitateur s’accorde avec la fréquence du pendule, les oscillations vont augmenter de plus en plus. C’est ce que l’on appelle la résonance.
Voici le modèle réalisé grâce à Stella :

Données introduites :
Résultat garphique de la position en fonction du temps :

On remarque clairement que les oscillations augmentent de plus en plus.
Pour conclure je vous invite à consulter quelques pages web en relation avec les oscillations :
– Oscillateur harmonique
– Pendule à ressort
– Oscillateur (libre, forcé et amorti)
