Étude de la variation de la période d’un pendule
par Antonin Urner, David Optyker, Théo Cormon
Un pendule qui se balance a un rythme très régulier. Tout les deux balancement, le pendule effectue une période et cette période pourrait dépendre de son amplitude, de sa longueur ou encore de sa masse...
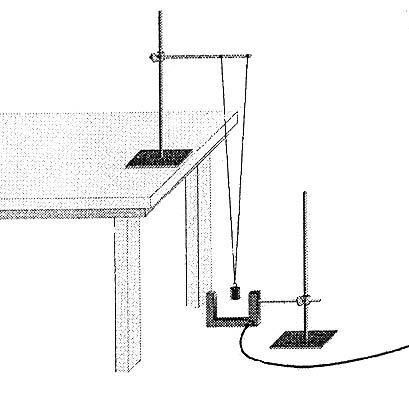
Objectifs : mesurer la période d’un pendule en fonction de son amplitude, de sa longueur ainsi que de sa masse.
Matériel : - ordinateur - LoggerPro - Mathematica - LabPro -rapporteur - ficelle - tiges, noix de fixation - règle graduée - grafical analisis
Question préalable : La période du pendule dépend-elle de sa masse, de son amplitude et ou de sa longueur ?
Suite à quelques observations visuelle sur la façon dont se balance le pendule, nous avons émis l’hypothèse que la période du pendule ne dépend ni de sa masse ni de son amplitude mais de sa longueur.
Procédure : Nous avons mesuré précisément la variation des périodes d’un pendule lorsque l’on modifie sa masse, son amplitude ou encore sa longueur.
Résultats obtenus :
– Variation de la période lorsque l’on modifie l’amplitude du pendule.

– Variation de la période lorsque l’on modifie la longueur du pendule.
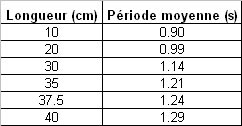
– Variation de la période lorsque l’on modifie la masse du pendule.
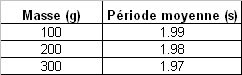
Analyse des résultats :
1) Pourquoi Logger Pro est-il réglé pour mesurer la durée séparant deux blocages du faisceau du portail ? Pourquoi pas la durée entre chaque blocage ?
Car pour qu’une période soit complète, il faut que le pendule passe dans le même sens devant la cellule.
2) Avec Mathematica, faites un graphique de la période en fonction de l’amplitude. La période dépend-elle de l’amplitude ?
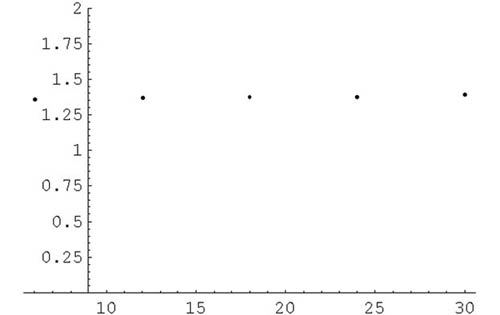
La période ne dépend pas ou très peu de l’amplitude. Car avec une grande amplitude le pendule ira plus vite et parcourra une plus grande distance. Alors qu’avec une petite amplitude, il ira moins vite et parcourra une plus petite distance. Donc le temps nécessaire pour effectuer une période sera identique.
3) Avec Mathematica, faites un graphique de la période en fonction de la longueur. La période dépend-elle de la longueur ?
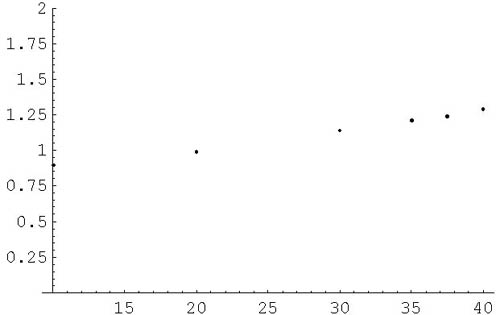
La période dépend de la longueur car avec une grande longueur, l’extrémité du pendule parcourt une grande distance avec une certaine vitesse qui ne change pas lorsque l’on modifie la longueur. Alors qu’avec une petite longueur, la distance parcourue par l’extrémité du pendule est plus petite. Nous pouvons donc conclure que plus la longueur est grande, plus la période sera grande.
4) Avec Mathematica, faites un graphique de la période en fonction de la masse. La période dépend-elle de la masse ? Avez-vous assez de données pour en être sûr ?
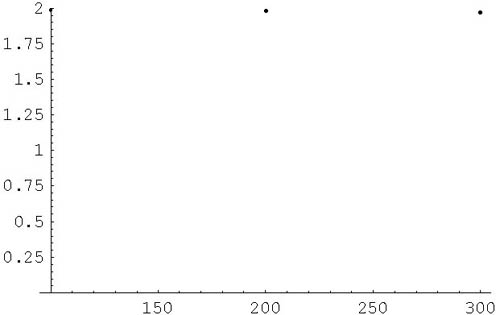
La période ne semble pas dépendre de la masse mais pour en être sûr, il faudrait effectuer d’autres mesures avec des poids ayant des différences plus grandes.
5) Pour examiner en détail comment la période dépend de la longueur, créez les deux graphiques suivants à partir de vos données :
- la période élevée au carré en fonction de la longueur.

- la période en fonction de la longueur élevée au carré.
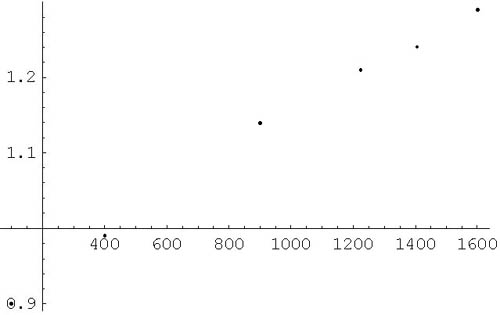
Lequel de ces deux graphiques est-il le plus proche d’une proportionnalité directe ?
Le graphique représentant la période en fonction de la longueur élevée au carré nous semble être celui qui se rapproche le plus d’une proportionnalité directe. Car les points sont alignés et la droite formée par ces points semble passer par l’origine.
6) A partir des lois de Newton, on peut montrer que pour certains pendules, la période “T” est liée à la longueur “l” et à l’accélération de la pesanteur “g” par :
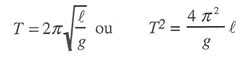
Un des des graphiques précédents est-il conforme à cette relation ?
Comme les lois de Newton font dépendre la longueur de la période élevée au carré, nous pouvons en déduire que le graphique qui fait dépendre la période élevée au carré en fonction de la longueur est le plus conforme à cette relation.
Conclusion : nous sommes globalement satisfaits de nos résultats car ils confirment notre hypothèse de départ, à savoir que la période d’un pendule dépend de sa longueur. Par contre nous avons été surpris que ce ne soit pas les mêmes graphiques qui correspondent aux questions 5) et 6).
Il faut prendre en compte que des erreurs ont pu êtres commises lors des mesures de longueurs du pendule.