
La méthode de Newton est une procédure classique pour résoudre des équations par approximations successives. Ce type de résolution est très ancien. Les Grecs en utilisaient déjà une variante pour trouver les racines carrées : on part d’une estimation ; cette estimation en fournit une meilleure, et, en réitérant le procédé, on obtient une valeur qui converge vers la solution. Ce procédé est rapide car le nombre de décimales gagnées en précision double en général à chaque étape. La répétition étant le point fort des ordinateurs, le procédé fait merveille en informatique, où il s’applique à une grande variété de problèmes. La méthode de Newton présente toutefois un petit inconvénient : la solution trouvée dépend de l’estimation initiale. Et comme les équations peuvent posséder plusieurs solutions, on n’obtient pas toujours celle que l’on cherche ! Mais cela ne fait en général pas problème, car on a une bonne idée de l’endroit où débuter, et, si la première tentative converge vers une solution inattendue, on peut toujours recommencer avec une autre estimation.
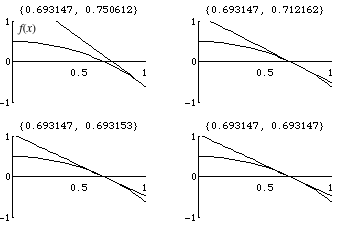
Voir aussi : Newton’s Method from the Wolfram Demonstrations Project.
