Brève description du sujet. Exemple illustré d’application (avec code). Réponses aux questions posées (avec démarche et code utilisés). Mention des sources et une référence.
par Antonio Rodriguez Pupo
Dans cet article, nous décrivons ce qu’est une transformation affine du plan, nous en donnons un exemple, et, afin d’adopter une démarche didactique, nous nous posons des questions de départ ; à la fin, les réponses, si l’article est clair est concis, permettent de synthétiser l’essentiel du sujet.
Le but étant surtout d’utiliser un outil informatique pour traiter un problème mathématique.
Plan
Questions
- Qu’est-ce qu’une transformation affine ?
- A quoi peut-elle bien servir ? Dans quels domaines trouvent-elles leur utilité ?
Description
Une transformation affine f du plan associe à chaque point (x ; y), le nouveau point (x’ ; y’) = f((x ; y)) = (αx + βy ; γx + δy) + (μ ; λ). On l’écrit généralement sous la forme matricielle :
$ \left( \begin{array}{cc} x’ \\ y’ \end{array} \right) = f((x ;y)) = \left( \begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{array} \right) \left( \begin{array}{cc} x \\ y \end{array} \right) + \left( \begin{array}{cc} \mu \\ \lambda \end{array} \right) $
"C’est Euler, en 1748, qui est à l’origine du terme « transformation affine », car dit-il, « deux courbes images l’une de l’autre par une telle transformation présentent entre elles une certaine affinité ».
De nos jours, une application affine est une application entre deux espaces affines qui préserve la structure affine, c’est-à-dire qui envoie les droites, plans, espaces,... en des droites, plans, espaces, ... tout en préservant la notion de parallélisme." (Wikipedia)
Il s’agit tout d’abord de rappeler quelques concepts basiques d’algèbre linéaire.
Un espace vectoriel sur ℜ est un triplet (E,+,•) formé d’un ensemble E, d’une opération interne E, notée + et d’une multiplication par un scalaire notée • satisfaisant les 8 axiomes suivants :
Addition : Pour tout élément u, v et w de E, on a
- (u+v) + w = u + (v+w)
- u + v = v + u
- Il existe un élément neutre noté o tel que u + o = u
- Pour chaque élément de E, il existe un élément opposé noté -u tel que u + (-u) = o
Multiplication Scalaire : Pour tout élément u et v de E, et tout nombre réel λ et μ, on a
- (λμ) • u = λ • (μ • u)
- (λ + μ) • u = λ • u + μ • u
- λ • (u+v) = λ • u + λ • v
- 1 • u = u
7 Propriétés :
- Si u + v = u + w, alors v = w
- 0 • u = o 0 ∈ ℜ et o ∈ E
- (-1) • u = -u
- Si (u ≠ 0 et λ • u = μ • u) ⇒ λ = μ
- λ • (u - v) = λ • u - λ • v
- (-λ) • (-u) = λ • u
- λ • u = o ⇔ (λ = 0 ou u = o)
On considère un espace vectoriel (E,+,•) de dimension n.
L’application f de E vers E est un endomorphisme de E si et seulement si :
f(u+v) = f(u) + f(v) et f(λu) = λf(u)
pour tout u et v de E et tout λ de ℜ.
Un endomorphisme f de E est une application linéaire de E vers E.
Un endomorphisme de E est aussi appelé transformation linéaire de E.
- Si f est un endomorphisme quelconque de ℜ2, alors il existe des réels α, β, γ et δ tels que f((x ;y)) = (αx + βy ; γx + δy)
- Si f est un endomorphisme quelconque de ℜ3, alors il existe des réels α1, α2, α3, β1, β2, β3, γ1, γ2 et γ3 tels que f((x ;y ;z)) = (α1x + β1y + γ1z ; α2x + β2y + γ2z ; α3x + β3y + γ3z)
Ces réels forment la matrice carrée M(f) associée à la fonction f relativement à la base canonique. On peut alors écrire :
Y = M(f) • X
où,
– Y est la matrice-colonne associée à f((x ;y))
– X est la matrice-colonne associée à (x ;y)
Exemple :
$ Y = M(f) . X = \left( \begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{array} \right) \left( \begin{array}{cc} x \\ y \end{array} \right) = \left( \begin{array}{cc} 1 & 2 \\ -4 & 3 \end{array} \right) \left( \begin{array}{cc} x \\ y \end{array} \right) = \left( \begin{array}{cc} x + 2y \\ -4x + 3y \end{array} \right) $
Le code Mathematica correspondant à cette explication théorique est le suivant (à copier-coller, puis exécuter dans l’ordre) ; ici vous trouvez l’expression de Y :
Exemples d’application
Pour effectuer une transformation affine du plan, nous nous servons de la matrice carré d’ordre 2 M(f), dont nous appliquons les réels à une liste de points (x ;y) afin d’obtenir une liste appliquée (x’ ;y’).
La première liste de points reportés sur un axe peut ainsi représenter une image et la liste appliquée sa transformation affine.
Nous souhaiterions "déformer" quelque peu un cercle trigonométrique.
Nous définissons d’abord le cercle trigonométrique par la liste PTest et, au besoin, le représentons graphiquement avec une ListPlot :
Nous définissons ensuite la matrice M(f) ainsi que la fonction f(x ;y).
Grace à Map, nous appliquons la fonction f à l’ensemble des points (x ;y) de la liste PTest. Il nous suffit de préciser (dans une liste de substitution interne /.) les réels α, β, γ et δ formant M(f) et qui permettent la transformation affine du cercle de départ d’avoir lieu.
Les points ainsi appliqués par Map sont représentés graphiquement par un ListPlot dans lequel nous ajoutons les options :
- AspectRatio -> Automatic afin d’avoir une image orthonormée
- PlotJoined -> True afin que les points reliés forment bien un cercle
- PlotStyle -> (Hue[2/3], Thickness[0.005]) afin d’avoir le tracé en bleu (Hue[2/3]) et les points d’une certaine épaisseur (Thickness[0.005]).
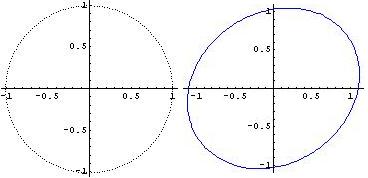
$ M(f) = \left( \begin{array}{cc} -1 & 0.5 \\ 0.3 & 1 \end{array} \right) $
Le résultat est bien ce que l’on escomptait :
– un graphique montrant la transformation du premier cercle trigonométrique.
Nous souhaiterions "déformer" et "agrandir" un smiley.
Nous définissons d’abord le Smiley par la liste PSmiley. Pour obtenir cette liste, nous créons les points manuellement en maintenant simultanément Ctrl + Clic Gauche en déplaçant le curseur afin de "dessiner" une série de points pris sur un graphique simple Gs défini par une droite.
Nous spécifions un repère orthonormé (AspectRatio -> Automatic) grâce auquel nous dessinons un Smiley de rayon à peu près égal à 40. Nous obtenons les points constituant ce Smiley.
Il s’agit ensuite de définir une matrice M(g), similaire à la matrice M(f) de l’exemple précédent.
Nous associons à cette matrice la fonction g(x ;y) qui comporte une spécificité par rapport au cas du cercle trigonométrique.
Il s’agit de l’addition de la matrice-colonne (μ ; λ). Cette dernière va nous permettre d’agrandir notre smiley (translater ses points), en complément à M(g) qui ne fait que le transformer (modifier ses points).
Nous pouvons vérifier que g[(x ;y)] est bien définie.
Puis nous appliquons avec Map la fonction g à la liste de points PSmiley constituant notre figure initiale. Nous spécifions les valeurs des réels α, β, γ, δ, μ et λ dans une liste (/.()) de substitution. Afin d’avoir une représentation graphique de l’application, nous insérons cela dans un ListPlot avec les options suivantes :
- AspectRatio -> Automatic afin d’avoir une image dans un repère orthonormé
- PlotStyle -> (Hue[2/3], Thickness[0.001]) afin d’avoir le tracé en bleu (Hue[2/3]) et les points d’une certaine épaisseur (Thickness[0.001]).
Nous pouvons comparer l’image obtenue par le code-ci dessus avec l’image initiale dont le code est le suivant :
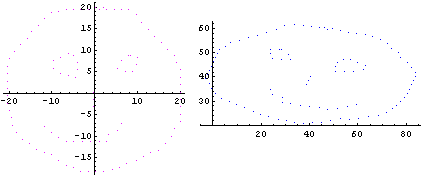
Notons qu’il ne s’agit rigoureusement pas d’une transformation linéaire car le vecteur translation (μ ; λ) n’est pas nul.
Nous voyons bien l’effet de translation du vecteur (μ ; λ) (en plus de celui de modification par M(g)).
Le Smiley initial se situe en effet de part et d’autre des axes x et y alors que le Smiley final a bien été translaté de μ=40 et λ=40, soit de 40 en abscisses comme en ordonnées.
Différence fondamentale entre l’exemple 1 et 2
Rigoureusement :
- les réels α, β, γ et δ formant M(g) caractérisent la modification
- les réels μ et λ définissent quant à eux latranslation
- On ne parle de transformation linéaire que lorsque les vecteurs translation sont nuls.
- L’exemple 1 est donc une transformation linéaire, alors que l’exemple 2 n’en est pas rigoureusement une.
Réponses aux questions posées
– 1. Qu’est-ce qu’une transformation affine ?
Une transformation affine f du plan, associe à chaque point (x ; y), le nouveau point :
f((x ;y)) = (αx + βy ; γx + δy) + (λ ; μ) = (αx + βy + λ ; γx + δy + μ )
Les réels α, β, γ et δ de la matrice carrée d’ordre 2 M(f) caractérisent la modification du plan, alors que les réels (λ ; μ) caractérisent une éventuelle translation de ce dernier.
N.B. : Nous avons à faire à une transformation linéaire ou endomorphisme que lorsque le vecteur (λ ; μ) est nul.
– 2. Dans quels domaines trouvent-elles leur utilité ? A quoi peut-elle bien servir ?
Les transformations affines sont très utiles en relativité galiléenne comme générale.
"La transformation de Galilée et la transformation de Lorentz peuvent s’exprimer à l’aide de matrices. La transformation de Galilée s’obtient comme limite de la transformation de Lorentz lorsque la vitesse de la lumière tend vers l’infini. La transformation de Lorentz peut s’interpréter comme une « rotation » dans un espace hyperbolique." (Cours de Physique)
Dans la série d’exercices sur les transformations exprimées à l’aide de matrices, il s’agit bien d’utiliser une matrice (similaire à M(f)) dans une transformation affine du plan et de résoudre l’équation :
$ Coordonnées_{\Sigma}*Matrice_{transformation} = Coordonnées_{\Sigma’}$
N.B. Le symbole * correspond ici à un produit matriciel.
Connaissant les coordonnées dans Σ et Σ’, il suffit alors de résoudre l’équation pour trouver la matrice de transformation.
Sources et Références
- http://fr.wikipedia.org/wiki/Application_affine
- http://www.owl-spip.ch/spip.php?breve242
- http://www.owl-spip.ch/spip.php?breve797
- http://www.owl-spip.ch/spip.php?article105
- Cours de Maths (algèbre linéaire)
- Cours d’application des maths du 13 Sept 2007
