par Jérémie Jaccard, Tiago Morais
Il y a deux manières de mesurer la raideur d’un ressort : la méthode statique et la méthode dynamique. Dans l’une on mesure la déformation du ressort (élongation ou encore altération de la position d’équilibre) avec différentes masses. L’autre consiste en la mesure de la période d’oscillation d’une masse.
Expérience
Oscillateur harmonique
1.
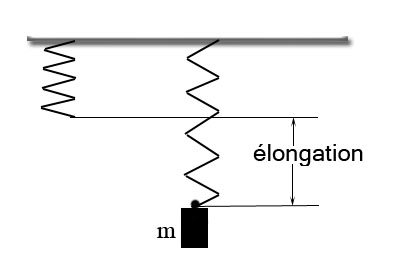
| Masse m | Elongation |
|---|---|
| 0.0 | 0.0 |
| 10 | 0.033 |
| 20 | 0.066 |
| 50 | 0.165 |
| 70 | 0.232 |
| 100 | 0.331 |
| 120 | 0.401 |
| 150 | 0.492 |
Les mesures sont respectivement en grammes[g] et en mètres[m]
2.
Pour trouver la raideur, il suffit de diviser la force par l’élongation pour obtenir des Newtons par mètre
| Force | Elongation | Raideur calculée |
|---|---|---|
| 0.0 | 0.0 | - |
| 0.0981 | 0.033 | 2.973 |
| 0.1962 | 0.066 | 2.973 |
| 0.4905 | 0.165 | 2.973 |
| 0.6867 | 0.232 | 2.960 |
| 0.981 | 0.331 | 2.964 |
| 1.1772 | 0.401 | 2.936 |
| 1.4715 | 0.492 | 2.991 |
Mesures en : Newtons[N], mètres[m] et Newtons par mètre[N/m]
Raideur k moyenne : 2.96714
3.
Après avoir suspendu une masse m de 30 g à deux ressorts différents, nous obtenons pour le premier ressort une période d’oscillation de :
T1=0.69[s] ( n=15 périodes)
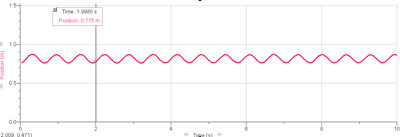
et pour le deuxième ressort une période de :
T2=0.33[s] ( n=29 périodes)

4.
Pour trouver les constantes k des deux ressorts nous allons utiliser la formule :
donc
Avec m=0.03 [kg] et T1=0.69 [s]
k=2.48 N/m
puis avec T2=0.33
k=10.88 N/m
5.
Pour doubler la période il faut quadrupler la masse du fait que m est sous une racine carrée ce qui nous donne une masse de 120 g.
Vérifions expérimentalement notre pronostic en suspendant au même ressort une masse de 120 g.
T1= 1.31 s Valeur attendue : 1.38 s => Incertitudes : abs. : 0.07 s relat. : 5.07% ( n=7 périodes)
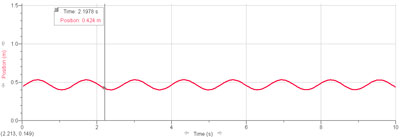
T2=0.64 s Valeur attendue : 0.66 s => Incertitudes : abs. : 0.02s relat. : 3.125% ( n=14 périodes)
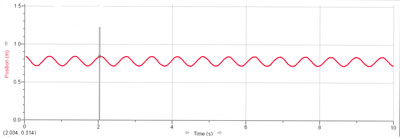
Nous remarquons qu’en quadruplant la masse, la période double (nous obtenons le double des valeurs précédentes).
Questions
1.
Equation différentielle de l’oscillateur harmonique :
avec
donc
L’équation différentielle de l’oscillateur harmonique admet effectivement comme solution
2.
A représente une amplitude, la distance entre la position de repos de l’oscillateur harmonique et le sommet de son oscillation (v=0). Cette grandeur se mesure en mètres.
3.
d’où :