par Jérémie Jaccard, Tiago Morais
En lançant une bille sur un plan incliné de manière perpendiculaire à sa trajectoire initiale, nous pouvons, à l’aide d’un carbone, transcrire cette dernière sur le papier. Le parcours de cette bille sera comparable celui d’un objet lancé dans les airs, à cela près qu’on pourra analyser de près le mouvement grâce à la trace laissée par la bille et le carbone sur le papier millimétré.
Outils requis :
- plan incliné avec rampe de lancement
- capteurs de départ et d’arrivée
- papier-carbone
- papier millimétré
- chronomètre
- bille
- WolframResearch Mathematica pré-installé sur un poste
Questions
1. Vous lancez une bille. Jusqu’où va-t-elle ? Comment doit-on reformuler cette question pour pouvoir y répondre ? Que doit-on connaître ?
Quelle distance la bille aura-t-elle parcourue ? La réponse à cette question requiert la connaissance (ou la mesure) de la vitesse initiale de la bille ainsi que son accélération (dépendant de la pente du plan dans le cas présent).
2. De quoi dépend l’accélération d’une bille se déplaçant sans frottement sur un plan incliné ?
Dans le cadre d’un mouvement non influencé par les frottements, l’accélération ne dépend que de la pente du plan incliné. On obtient la formule suivante :
$a = \frac{m*g*sin(\alpha)}{ m} <=> a=g*sin(\alpha)$
On remarque que les masses s’annulent, laissant ainsi comme seule influence l’inclinaison du plan.
3. La vitesse initiale d’une bille lancée en l’air ou sur un plan incliné modifie-t-elle son accélération ?
Comme nous l’avons vu plus haut la seule chose qui peut modifier l’accélération est l’inclinaison du plan. Par conséquent, la seule réponse possible est non.
4. En quoi le mouvement d’une bille lancée en l’air et celui d’une bille lancée sur un plan incliné sont-ils comparables ?
Les deux mouvements sont attirés par une force constante et dirigée perpendiculairement à l’axe Ox. Dans les deux cas la force de gravitation joue un grand rôle. Pour finir, les deux trajectoires des deux mouvements sont de type parabolique et peuvent ainsi s’écrire sous la forme d’une équation horaire d’un tir parabolique plus précisément d’un MUA [1] :
$\vec r (t)= \vec r_{0} + \vec v_{0}t + \frac{1}{2} \vec a t^{2}$
Expérience
Premier point de départ :
La bille a un temps de chute moyen de 0.67 s et passe par ces points :
| Y | X |
|---|---|
| 0 m | 0 m |
| 0.55 m | 0.113 m |
| 0.105 m | 0.161 m |
| 0.155 m | 0.198.5 m |
| 0.205 m | 0.230 m |
| 0.255 m | 0.258 m |
| 0.305 m | 0.283 m |
Deuxième point de départ :
La bille a un temps de chute moyen de 0.67 s et passe par ces points :
| Y | X |
|---|---|
| 0 m | 0 m |
| 0.55 m | 0.075 m |
| 0.105 m | 0.1085 m |
| 0.155 m | 0.134 m |
| 0.205 m | 0.1545 m |
| 0.255 m | 0.1735 m |
| 0.305 m | 0.190 m |
NB : On peut observer que le temps de chute ne dépend pas de la vitesse initiale.
Trajectoire en DAO [2]
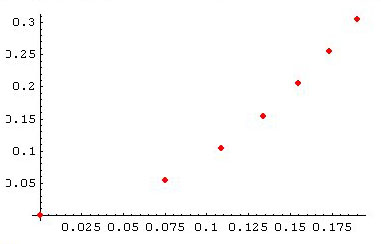
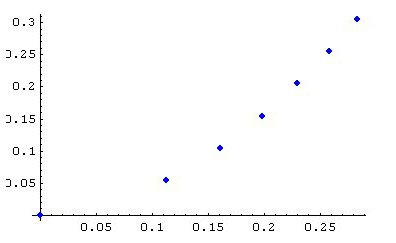
Les courbes optimales obtenues avec ces points :
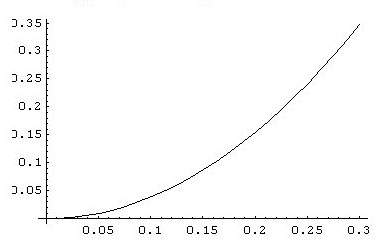
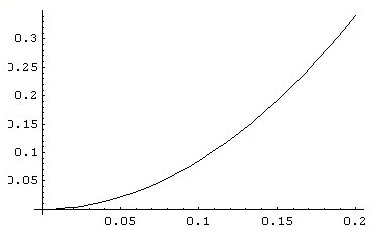
NB : les échelles sont adaptées aux points (ou aux courbes)
Manipulation des résultats
Equation :
Pour le premier point de départ on a :
$\vec r (t)= \vec r_{0} + \vec v_{0}t + \frac{1}{2} \vec a t^{2}$
Pour le deuxième point de départ on a :
$\vec r (t)= \vec r_{0} + \vec v_{0}t + \frac{1}{2} \vec a t^{2}$
Accélération
Dans le cas présent, on observe un tir parabolique. En négligeant les frottements, on pourrait décomposer la vitesse en deux composantes selon x et y. Pour l’axe des abscisses (ci-après Ox) la vitesse est constante il n’y a donc pas d’accélération. Pour ce qui est de l’axe des ordonnées (ci-après Oy) en revanche, l’accélération se note sous
la forme suivante : $ y = - \frac{1}{2} a_{y} t^{2} $ ainsi, $ a_{y} = - \frac{2 y}{t^{2}} $
d’où :
première bille $ a_{y} = - \frac{0.61}{0.67^{2}}= 1.359 m/s^{2} $ ainsi, $ \vec a = (0 ;1.359) m/s^{2} $
la seconde bille ayant une accélération égale, $ \vec a = (0 ;1.359) m/s^{2} $
Vitesses :
-Initiale :
Pour calculer la vitesse il faut la décomposer selon l’axe Ox et l’axe Oy. La vitesse selon l’axe Ox est un MRU [3] donc est constante et selon l’axe Oy est nulle. Ainsi on obtient :
– Premier point de départ :
$ V_{0x} = \frac{d}{t} $
$ V_{0x} = \frac{0.283}{0.69} = 0.41 \frac{m}{s}$
– Deuxième point de départ :
$ V_{0x} = \frac{d}{t}$
$ V_{0x} = \frac{0.190}{0.69} = 0.275 \frac{m}{s}$
-Finale :
La vitesse finale doit aussi se décomposer selon les deux axes. Selon l’axe Ox nous avons déjà vu que elle est un MRU et selon l’axe Oy est un MRUA [4], on l’obtient en dérivant l’équation : $\vec r (t)= \vec r_{0} + \vec v_{0}t + \frac{1}{2} \vec a t^{2}$ .
Ainsi on a :
$ V_{yfin} = a_{y}*t$
$V_{yfin} = 1.359*0.69 = 0.938 \frac{m}{s} $
Le temps de chute est le même selon l’axe Ox et Oy, car la vitesse initiale selon Ox n’influence pas l’accélération et donc comme nous l’avons vu plus haut, rien n’influence le mouvement de la bille, si ce n’est la pente qui, au long de l’expérience ne varie pas. Ainsi on a :
Premier point de départ :
$ \vec V_{fin} = (0.41 ;0.938) m/s$
Deuxième point de départ :
$ \vec V_{fin} = (0.275 ;0.938) m/s $
Conclusion :
Nous remarquons que Mathematica nous fournit automatiquement les réponses exactes avec plus de précision que nous ne saurions le faire.
Constatons cependant qu’il est quand même possible de trouver toutes les réponses, moins précises certes, mais sans avoir recours aux moyens informatiques.
