Expérience

Oscillateur harmonique

1.

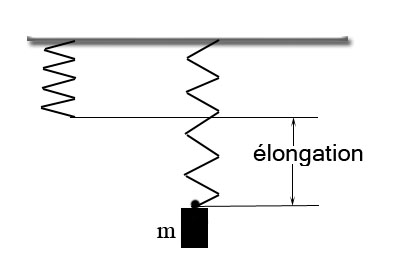
Masse m	Elongation
0.0	0.0
10	0.033
20	0.066
50	0.165
70	0.232
100	0.331
120	0.401
150	0.492

Les mesures sont respectivement en grammes[g] et en mètres[m]

2.
Pour trouver la raideur, il suffit de diviser la force par l’élongation pour obtenir des Newtons par mètre

Force	Elongation	Raideur calculée
0.0	0.0	-
0.0981	0.033	2.973
0.1962	0.066	2.973
0.4905	0.165	2.973
0.6867	0.232	2.960
0.981	0.331	2.964
1.1772	0.401	2.936
1.4715	0.492	2.991

Mesures en : Newtons[N], mètres[m] et Newtons par mètre[N/m]

Raideur k moyenne : 2.96714

3.
Après avoir suspendu une masse m de 30 g à deux ressorts différents, nous obtenons pour le premier ressort une période d’oscillation de :

T1=0.69[s] ( n=15 périodes)

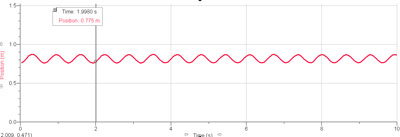
et pour le deuxième ressort une période de :

T2=0.33[s] ( n=29 périodes)

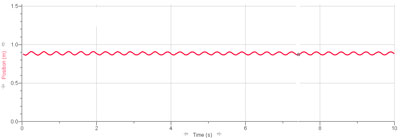
4.

Pour trouver les constantes k des deux ressorts nous allons utiliser la formule :

$ T= 2\pi*\sqrt{m/k}$

donc

$k=m/(T/2\pi)^{2}$$$

Avec m=0.03 [kg] et T1=0.69 [s]

k=2.48 N/m

puis avec T2=0.33

k=10.88 N/m

5.

$$$2*T=2*2\pi\sqrt{m/k}$

$2*T=2\pi\sqrt{4m/k}$$$

Pour doubler la période il faut quadrupler la masse du fait que m est sous une racine carrée ce qui nous donne une masse de 120 g.

Vérifions expérimentalement notre pronostic en suspendant au même ressort une masse de 120 g.

T1= 1.31 s Valeur attendue : 1.38 s => Incertitudes : abs. : 0.07 s relat. : 5.07% ( n=7 périodes)

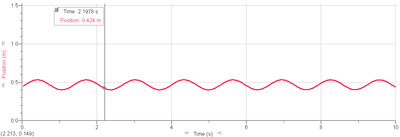
T2=0.64 s Valeur attendue : 0.66 s => Incertitudes : abs. : 0.02s relat. : 3.125% ( n=14 périodes)

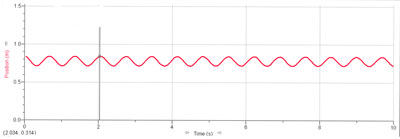
Nous remarquons qu’en quadruplant la masse, la période double (nous obtenons le double des valeurs précédentes).

Questions

1.
Equation différentielle de l’oscillateur harmonique :

$$$ mx’’(t)=-kx(t)$

avec $ x(t)= Asin(\omega*t+\phi) $ et $x’’(t)=-\omega^{2}Asin(\omega*t+\phi)$

donc

$-m\omega^{2}Asin(\omega*t+\phi)=-kAsin(\omega*t+\phi)$

$m\omega^{2}Asin(\omega*t+\phi)-kAsin(\omega*t+\phi)=0$

$Asin(\omega*t+\phi)*[m\omega^{2}-k]$

L’équation différentielle de l’oscillateur harmonique admet effectivement comme solution $ x(t)= Asin(\omega*t+\phi) $

2.
A représente une amplitude, la distance entre la position de repos de l’oscillateur harmonique et le sommet de son oscillation (v=0). Cette grandeur se mesure en mètres.

$\omega$$représente\; une\; vitesse\; angulaire,\; une\; vitesse\; de\; rotation.\; Celle-ci\; s’exprime\; en\; rad/s\; (\; radians\; par\; seconde\; ).$

$$$\phi$$quant\; à\; lui\; symbolise\; un\; déphasage,\; une\; écart\; entre\; la\; position\; initiale\; et\; le\; zéro\; "commun".\; Ce\; dernier\; se\; calcule\; en\; radians.$

3.
$$$T=2\pi/\omega$ et $\omega=\sqrt{k/m}$

d’où :

$T=2\pi\sqrt{m/k}$