Mesure des temps de chute d’une bille en fonction de la hauteur et détermination de son accélération.
La mesure du temps de parcours d’une bille pour différentes hauteurs de chute permet de déterminer son accélération. Pour une bille en acier et des hauteurs de l’ordre du mètre, on peut négliger la force de frottement due à l’air et l’accélération obtenue correspond à l’accélération terrestre.
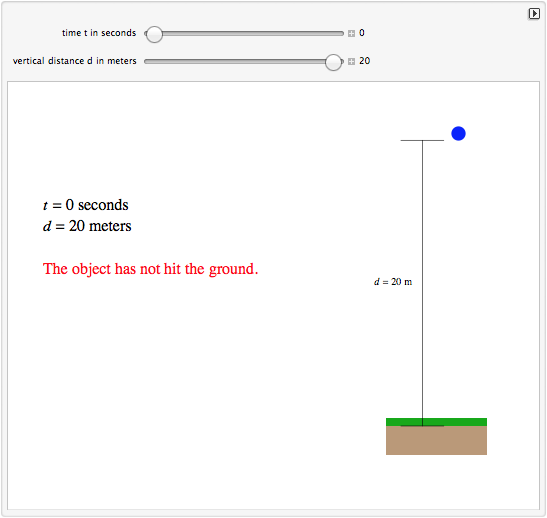
Utiliser le modèle (nécessite Wolfram CDF Player)
Au voisinage de la surface terrestre, tous les corps qu’on laisse tomber et pour lesquels on peut négliger la force de frottement due à l’air, s’accompagnent dans leur chute : ils subissent la même accélération qui vaut environ 10 m/s2. Cela signifie que leur vitesse augmente chaque seconde de 10 m/s. Ainsi, la vitesse d’un objet qui chute et dont la vitesse initiale est nulle vaut, après 1 seconde, 10 m/s, après 2 secondes, 20 m/s, etc. Si l’objet est lancé verticalement vers le bas avec une vitesse initiale v0, sa vitesse v après t secondes de chute vaut v=v0+at. Si l’objet est lancé verticalement vers le haut avec une vitesse initiale v0, il subit toujours la même accélération, mais cette fois la vitesse et l’accélération sont de sens opposés. La vitesse de l’objet diminue et après t secondes elle vaut v=v0-at.

Accélération d’une bille : mouvements descendant et ascendant. Dans les deux cas, le vecteur accélération est le même.
Pour ces mouvements verticaux qui sont des mouvements uniformément accélérés (i.e des mouvements pour lesquels l’accélération est constante), nous obtenons des droites si nous reportons la vitesse en fonction du temps. La pente de ces droites donne l’accélération.

Horaire de la vitesse : la vitesse en fonction du temps pour des mouvements uniformément accélérés est donnée par une droite. La pente de la droite donne l’accélération du mouvement.
A partir d’un graphique donnant la vitesse d’un mobile en fonction du temps, il est possible d’obtenir la distance parcourue. Le cas le plus simple est celui dans lequel la vitesse est constante. Nous savons que la distance parcourue s’obtient en multipliant la vitesse v par le temps t.
Graphiquement, cela revient à calculer la surface comprise entre la droite v=v(t) et l’axe t. Pour les mouvements uniformément accélérés ci-dessus, nous obtenons, si nous exprimons les aires des triangles, d=vt/2, qui est la distance parcourue en un temps t. La vitesse v du mobile est plus difficile à mesurer que le temps de chute t. Nous exprimons donc la vitesse en fonction du temps v=at, ce qui donne, pour la distance parcourue d= at2/2.

L’horaire de la vitesse permet de trouver la distance parcourue qui est donnée par l’aire en grisé.
Expérience
- Mesurez le temps de chute d’une bille pour 6 hauteurs différentes. Répétez 4 fois la mesure pour chaque hauteur et calculez le temps de chute moyen.
- Reportez les hauteurs de chute en fonction des temps de chute moyens élevés au carré.
- Déterminez, à partir du graphique obtenu, l’accélération de ces mouvements.
- Calculez la vitesse finale de la bille pour chaque hauteur de chute.
- Reportez les vitesses finales calculées en fonction de la hauteur de chute (premier graphique), puis du temps de chute (deuxième graphique). Que constatez-vous ?
Questions
– Ecrivez l’équation horaire de la bille.
– Donnez les formules de la chute des corps permettant d’obtenir :
- la vitesse en fonction du temps et de l’accélération ;
- la vitesse en fonction du chemin parcouru et de l’accélération.
– Vous lancez une balle verticalement vers le haut. Dessinez le vecteur caractérisant l’accélération de la balle lorsque :
- elle s’élève ;
- elle a atteint le point le plus haut ;
- elle redescend.
– Pour un parachutiste, la force de frottement due à l’air n’est pas négligeable. Sa vitesse finit par se stabiliser, même si le parachute reste fermé. Le graphique ci-dessous donne l’évolution de la vitesse d’un parachutiste (en m/s) en fonction du temps (en s). Estimez, à partir de ce graphique :
- l’accélération initiale du parachutiste ;
- la distance franchie par le parachutiste en 20 secondes.
- Comparez cette distance à celle qu’il aurait franchie sans frottement.

Vitesse d’un parachutiste en fonction du temps : lorsque le mobile est soumis au frottement de l’air, sa vitesse n’augmente plus linéairement avec le temps : elle tend vers une vitesse limite (asymptote horizontale).
Simulations (from The Wolfram Demontrations Project)
– Measuring Gravity at the Surface of the Earth
– Free Fall on the Solar System Planets and the Moon
– Integration Is a Sum