But

– Examiner les énergies mises en jeu dans un mouvement harmonique.
– Illustrer le principe de conservation de l’énergie.

Introduction

Nous pouvons décrire une masse oscillante en termes de position, de vitesse et d’accélération en fonction du temps. Nous pouvons aussi décrire le système du point de vue de l’énergie. Dans cette expérience, nous allons mesurer la position et la vitesse d’une masse accrochée à un ressort en fonction du temps, et à partir de ces données, nous allons établir les graphiques de l’énergie cinétique et de l’énergie potentielle du système.

Dans le système formé par la masse et le ressort, l’énergie est présente sous trois formes. La masse $m$, de vitesse $v$, peut avoir une énergie cinétique :

$E_c_i_n$=$\frac{mv^2}{2}$

Le ressort peut posséder de l’énergie potentielle élastique donnée par :

$E_é_l_a_s_t_i_q_u_e$=$\frac{1}{2}ky^2$

où $k$ est la constante du ressort et $y$ est l’extension ou la compression du ressort mesurée à partir de la position d’équilibre.

Le système formé par la masse et le ressort possède aussi de l’énergie potentielle de gravitation, mais nous n’avons pas besoin d’inclure ce terme si nous mesurons la longueur du ressort à partir de sa position d’équilibre. Nous pouvons donc nous concentrer sur l’échange d’énergie entre l’énergie cinétique et l’énergie potentielle élastique.

Si le système ne subit pas d’autres forces, alors le principe de conservation de l’énergie nous dit que la somme $\Delta E_c_i_n$+$\Delta E_é_l_a_s_t_i_q_u_e$=0, ce que nous pouvons tester expérimentalement.

Préalables

1. Faisons une esquisse du graphique de la hauteur $x$ de la masse en fonction du temps $t$ et indiquons à quels instants la masse se déplace le plus vite ( E_cinMax ) et le plus lentement ( E_cin=0 ) ainsi que une esquisse du graphique de la vitesse $V$ en fonction du temps $t$ :

La masse a la vitesse la plus élevée quand celle-ci atteint le point d’équilibre tandis qu’elle est minimum quand elle atteint le point culminant.
La masse a l’énergie potentielle la plus grande quand celle-ci se trouve au point culminant et elle a l’énergie potentielle la plus faible quand elle atteint le point d’équilibre.

2. Faisons l’esquisse du graphique de l’énergie potentielle$E_p_o_t$ et cinétique $E_c_i_n$ en fonction du temps $t$ :

Tableau des données

La constante du ressort a été calculée par à la loi de Hooke : $F=-k\Delta$$x$

Analyse

1. Graphique expérimentale de la vitesse $V$ et de la position $x$ en fonction du temps :

2. Graphique représentant l’énergie cinétique, potentielle et mécanique :

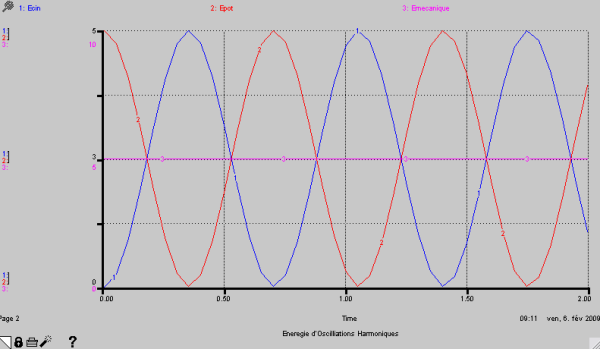
Sur le graphique ci-dessus nous remarquons que l’énergie cinétique est maximum quand l’énergie potentielle est minimum et vis versa c’est pourquoi l’énergie mécanique est constante. Nous pouvons donc écrire :

$E_m_é_c = E_c_i_n + E_p_o_t = constante$

Extension

– Faisons l’esquisse du graphique des énergies en fonction du temps $t$ dans un cas où le frottement n’est pas négligeable :

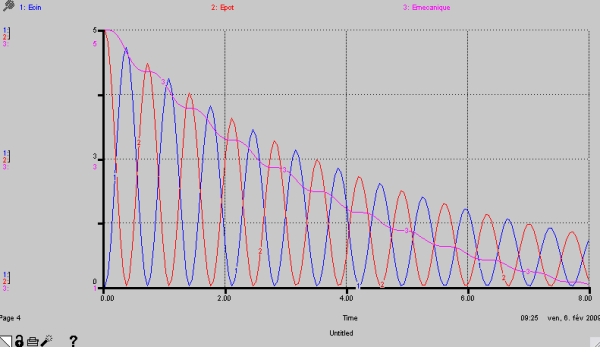
– Déterminons la position d’équilibre $s$ quand une masse $m$ est suspendue au ressort. Ce sera l’origine d’un nouveau référentiel avec la position $h$ :
Sachant que $F=mg$ et que $F=-k\Delta$$x$ on peut donc écrire :

$mg=-kx$

donc

$x=-\frac{mg}{k}$

Conclusion

Nous avons apprécié travailler sur ce phénomène, car celui-ci nous a permis de mieux comprendre le fonctionnement des différents types d’énergies dans le mouvement harmonique.

Source et lien

– Protocole de l’expérience