Rapport du 3 novembre sur la résistance de l’air
But :
– Etudier l’effet du frottement de l’air sur la vitesse d’un objet en chute verticale.
– Etudier la relation entre la masse et la vitesse limite d’un objet en chute verticale.
– Comparer les résultats expérimentaux à deux modèles différents décrivant la force de frottement fluide.
Méthode :
A l’aide d’un détecteur de mouvement, enregistrer l’horaire d’un cône en papier en chute verticale.
Manipulation et mesures :
– Nous avons pesé un cône en papier.
– Nous l’avons placé en-dessous d’un dédecteur de mouvement puis nous l’avons laissé tomber.
– A l’aide du logiciel Logger Pro qui était relié au détecteur, nous avons pu obtenir une droite de régression linéaire ainsi que la vitesse à l’aide de la pente.
– Nous avons répété cette expérience en empilant au fur et à mesure plusieurs cônes.
– Nous obtenons le tableau suivant :
| nombres de cônes | masse m en kg | vitesse v en m/s | vitesse au carré v² en m/s² |
| 1 | 0.00190 | 1.310 | 1.716 |
| 2 | 0.00381 | 2.019 | 4.076 |
| 3 | 0.00573 | 2.313 | 5.350 |
| 4 | 0.00763 | 2.580 | 6.656 |
| 5 | 0.00947 | 2.816 | 7.930 |
| 6 | 0.01085 | 2.829 | 8.003 |
| 7 | 0.01231 | 3.251 | 10.569 |
| 8 | 0.01375 | 3.222 | 10.381 |
| 9 | 0.01519 | 3.224 | 10.394 |
| 10 | 0.01664 | 3.395 | 11.526 |
Analyse des résultats :
– D’après la 1ère loi de Newton, la résultante des forces que subit l’objet, après avoir atteint sa vitesse limite (constante), est nulle. Si on suppose que les forces qui s’exercent sur cet objet durant sa chute sont sa force de pesanteur $F_{p}$ et sa force de frottement $F_{frott}$, alors elles ont la même intensité : $F_{p}=F_{frott}$
– On peut donc exprimer la relation entre la vitesse limite et la masse de l’objet.
- A faible vitesse, $-bv=mg$ où $v=v_{lim}$.
D’où : $v_{lim}\propto m$ - A vitesse élevée, $-cv^2=mg$ où $v=v_{lim}$.
D’où $v_{lim}^2\propto m$
– Pour déterminer laquelle de ces deux lois décrit le mieux nos données expérimentales, nous les avons représentés graphiquement :
- $v_{lim}\propto m$

- $v_{lim}^2\propto m$

On constate que dans le premier graphique les points sont plus éloignés de la droite moyenne et sont moins précis, alors que dans le deuxième graphique les points sont plus proches de la droite et sont plus précis ce qui correspond le mieux à nos données expérimentales. Nous utiliserons donc la deuxième loi : $v_{lim}^2\propto m$
– Pour trouver la valeur numérique du coefficient de proportionnalité dans cette loi, il faut partir de l’égalité suivante : $F_{p}=F_{frott}$
Donc : $-cv^2=mg$
Alors : $c=-\frac {mg}{v^2}$
D’où : $c=-\frac {0.00947*-9.81}{7.930}=0.011715\frac{kg}{m}$
Questions :
– Si on compare l’évolution de la vitesse au cours du temps d’un cône en papier et d’une balle de golf en chute verticale dont la résistance de l’air est nulle, on constatera que leur accélération est la même, soit l’accélération terrestre. On aura donc le même graphique qualitatif pour les deux objets :

– Schéma du cône à l’instant de sa chute avant d’avoir atteint sa vitesse limite :
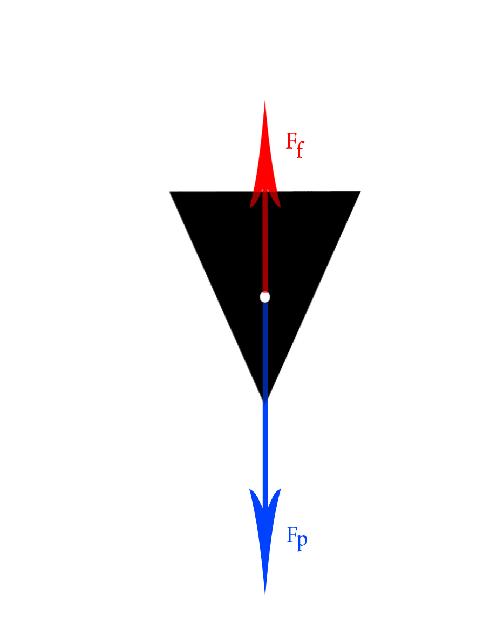
On remarque que la force de frottement est plus petite que la force de pensenteur.
– Schéma du cône à l’instant de sa chute ayant atteint sa vitesse limite :
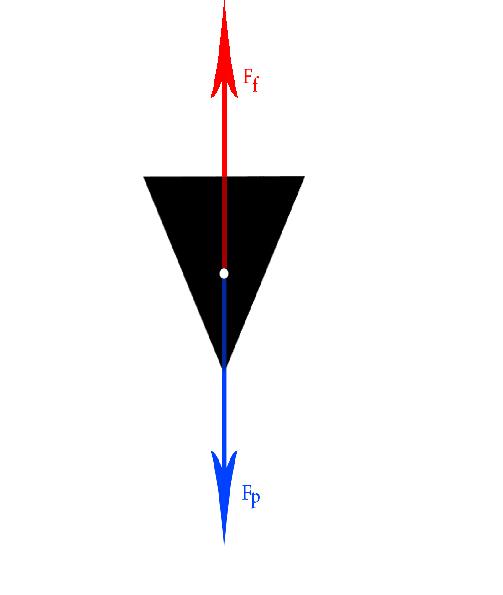
On remarque que la force de frottement est égale à la force de pensenteur.
– Pour trouver l’expression algébrique du temps de chute en fonction de sa masse d’après la relation $-bv=mg$, il faut remplacer $v$ en utilisant la formule : $v=\frac{d}{t}$
Donc : $-b\frac{d}{t}=mg$
Alors : $-bd=mgt$
D’où : $t=\frac{bd}{mg}$
– Pour trouver l’expression algébrique du temps de chute en fonction de sa masse d’après la relation $-cv^2=mg$, il faut remplacer $v$ en utilisant la formule : $v=\frac{d}{t}$
Donc : $-c\frac{d^2}{t^2}=mg$
Alors : $-cd^2=mgt^2$
D’où : $t=\sqrt{\frac{cd^2}{mg}}$
– Graphique de la chute d’un parachutiste :

Conclusion
Nous avons étudié l’effet du frottement de l’air sur la vitesse d’un objet en chute verticale, d’où nous avons pu conclure que la force de frottement de l’air freine la chute de l’objet et lui impose une vitesse limite.
On remarque aussi que la vitesse limite varie selon la masse de l’objet, c’est-à-dire que plus la masse de notre objet de chute est grande plus la vitesse limite sera grande.
À l’aide de nos résultats expérimentaux, nous avons conclu que le modèle de la vitesse au carré $v_{lim}^2\propto m$ était plus précis et correspondait mieux à nos résultats que le modèle de la vitesse $v_{lim}\propto m$.
