Latitude et longitude d’un point sur une sphère.
par bernard.vuilleumier
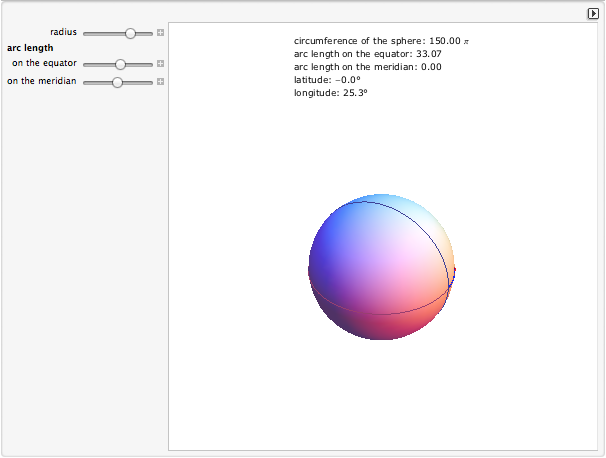
Utiliser le modèle (nécessite Wolfram CDF Player)
Tableau des notions et des activités
Présentation
La position d’un point sur une sphère, ou d’une ville sur Terre, peut être donnée par sa latitude et sa longitude. Ces deux grandeurs angulaires s’expriment en degré. La latitude se mesure depuis l’équateur vers les pôles Nord et Sud. La longitude se mesure depuis le méridien de Greenwich vers l’Est et vers l’Ouest.
Objectifs
– rechercher des informations dans des tables ou sur la toile
– utiliser les proportions
Notions
– angle
– arc de cercle
– proportion
– rayon d’un cercle
– relation entre l’arc, l’angle et le rayon
Matériel
– sphères en sagex
– clous (pour les pôles)
– fil
– ciseaux
– épingles et petits morceaux de papier
– ruban métrique
– calculatrice

Durée
– 2 fois 45 minutes
Activités
1. Relevez la latitude et la longitude de quelques villes (avec Google Earth)
2. Fixez les pôles Nord et Sud sur la sphère de sagex
3. Tendez un fil passant par les pôles et décrivant un grand cercle (méridien)
4. Placez pour chaque ville une épingle sur la sphère en polystyrène
5. Mesurez les distances séparant une épingle de chacune des autres
6. Calculez les distances correspondantes entre les villes
7. Estimez les incertitudes sur ces distances
8. Calculez les incertitudes relatives pour chacune d’elles.
Extension
– Trouvez la distance entre deux villes dont les latitudes et longitudes sont connues :
| Geneva | Bombay | Los Angeles | Sydney | |
|---|---|---|---|---|
| latitude | 31 | 19 | 9 | -33.9 |
| longitude | -85.9 | 72.8 | 125.6 | 151.2 |
| Geneva-Bombay | Geneva-Los Angeles | Geneva-Sydney | ||
| distances |
– Dessinez une sphère à l’aide de l’ordinateur et de Mathematica
– Placez les points correspondant aux villes retenues
– Calculez les distances séparant ces villes
– Trouvez le chemin le plus court reliant ces villes.
Quelques pistes pour l’évaluation [1]
– Distance sur une sphère : questions
– Distance sur une sphère : réponses aux questions