Une expérience permettant de calculer la masse d’un électron.
par Alexandre Cacheiro, Rodrigo de Pablo Pena, Romuald Hausser
Un canon envoie des électrons dans une boule de verre contenant de l’hydrogène qui rend la trajectoire des électrons visible. Un champ magnétique force les électrons à décrire un cercle. Grâce au rayon de ce cercle et à diverses équations physiques nous pouvons déterminer la masse des électrons.
Expérience :
Nous avons appliqué trois tensions U différentes dans un canon à électrons. Pour chacune d’elles, nous avons fait varier le courant I passant dans les bobines qui créent un champ magnétique entre 0.8 et 2.2 A. Nous avons ensuite mesuré le diamètre du cercle formé par les éléctrons.
?Mesures
Relevé des valeurs du diamètre des cercles d’électrons pour I variant de 0.8 à 2.2 A. Et pour U égal à 150 V, 200 V et 250 V.
| Ampère ¦ | ¦ 150 V ¦ | ¦ 200 V ¦ | ¦ 250 V |
|---|---|---|---|
| 0.8 | 13 cm | ? | ? |
| 1 | 10 cm | 12.3 cm | 13.3 cm |
| 1.2 | 8 cm | 10 cm | 11.2 cm |
| 1.4 | 7.3 cm | 8.8 cm | 10 cm |
| 1.6 | 6.5 cm | 7.7 cm | 8.5 cm |
| 1.8 | 5.7 cm | 6.8 cm | 7.6 cm |
| 2 | 5.1 cm | 6 cm | 7 cm |
| 2.2 | 4.4 cm | 5.4 cm | 6.3 cm |
?Calcul de k
Représentation Graphiques de r (rayon du cercle d’électrons) en fonction de 1/I pour les différentes tensions.
Tension = 150 V

Tension = 200 V

Tension = 250 V
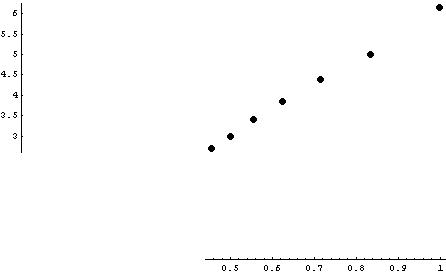
Sur le graphique nous voyons que ƒ(I) = r. Dans le Protocole, nous trouvons la formule suivante : r = k/I. La fonction est donc : ƒ(I) =k/I.
Nous connaissons r grâce aux mesures et nous connaissons I car il est dicté par le protocole. Nous pouvons donc trouver k : k = r*I.
Attention : sur les graphiques r est en centimètre, pour les calculs il faut utiliser les unités MKS.
| Ampère ¦ | ¦ 150 V ¦ | ¦ 200 V ¦ | ¦ 250 V |
|---|---|---|---|
| 0.8 | 0.06 | ? | ? |
| 1 | 0.05 | 0.0615 | 0.0665 |
| 1.2 | 0.048 | 0.06 | 0.0672 |
| 1.4 | 0.0511 | 0.0616 | 0.07 |
| 1.6 | 0.052 | 0.0616 | 0.068 |
| 1.8 | 0.0513 | 0.0612 | 0.0684 |
| 2 | 0.051 | 0.06 | 0.07 |
| 2.2 | 0.0484 | 0.0594 | 0.0693 |
| Moy | 0.051475 | 0.060757143 | 0.068485714 |
Voilà le tableau des k pour chaque rayon et la moyenne de k pour les différentes tensions.
150 V->0.051475
200 V->0.060757143
250 V->0.068485714
?Calcul de la masse de l’électron (m)
Nous avons estimé à 130 le nombre de spires (N) composant bobines qui créent le champ magnétique.
Le rayon des spires (R) est de 0.15 m.
La charge d’un électron est de 1.6*10^-19 C.
u0 = 4*$\pi$*10^-7, c’est la perméabilité du vide.
La formule suivante est tirée de notre protocole.
Nous isolons m/q à l’aide de Mathematica.
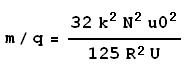
Calcul de m, la masse de l’électron, dans les 3 cas :
150 V-> 8.581936842*10^-31Kg
200 V-> 8.967028587*10^-31 Kg
250 V-> 9.114730446*10^-31 Kg
La valeur de la masse d’un électron de la table est de 9.10939*10^-31. Nous pensons que nos principales sources d’incertitudes sont l’estimation du nombre de spires des bobines et la mesure du diamètre du cercle d’éléctron.
?Calcul d’incertitude
Avec une incertitude de mesure de ± 1 cm pour le diamètre des cercles d’électrons.
Cela nous fait que le rayon (r) deux fois plus petit que le diamètre à ± 0.5 cm d’insertitude.
Cette incertitude dans la formule du k : k = r*I, nous donne un k à ± 0.0075.
Avec cette incertitude, on trouve une masse avec une erreur de ± 9%
Au niveau des spires, l’incertitude est totale, nous ne pouvions qu’en compter 15 et nous savions qu’il y en avait plus, en tout cas cinq fois plus. Nous avons choisi 130 car ce chiffre nous permet d’obtenir un résultat proche de la réalité. Mais nous mettons l’incertitude suivante :
N=130± 50
Cela nous donne une masse avec une erreur de ± 88%.
En combinant les deux incertitudes nous arrivons à une erreur de ± 109%.
Dans cette expérience, nous traitons des chiffres relativement grands dans le but de trouver un résultat minuscule. C’est pour cela qu’une petite erreur de mesure se répercute au final par une très grande différence dans le résultat.