– Champ : cinématique vectorielle
– Documents autorisés : Tables numériques CRM. Calculette.
– Vendredi 10 novembre 2006, CECNB, M1-M2, 95 min.
– Moyenne de classe : 5
– Écart type : 0.86
– Effectif : N=16

Problème 1 (7 points)

Un mobile a l’horaire suivant :

$\vec r (t)=\vec A t^2 + \vec B t,$ $\vec A=\begin{pmatrix}{0 \cr -1}\frac{m}{s^2},\end{pmatrix}$ $\vec B=\begin{pmatrix}{2 \cr 5}\frac{m}{s}\end{pmatrix}$

1. Exprimez l’horaire de sa vitesse et l’horaire de son accélération. (2 points)
2. Calculez, de seconde en seconde pour t variant de 0 à 4 s, les composantes (x, y) de son vecteur position $\vec r$, ($v_x, v_y$) de son vecteur vitesse $\vec v$ et ($a_x, a_y$) de son vecteur accélération $\vec a$. Présentez les résultats dans un tableau. (3 points)
3. Dessinez la trajectoire du mobile. (1 point)
4. A quel instant la vitesse du mobile est-elle parallèle à Ox ? (1 point)

Problème 2 (8 points)

L’accélération d’un véhicule qui part de l’arrêt est donnée par le graphique ci-dessous :

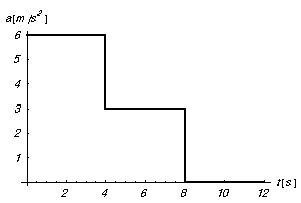
1. Dessinez le graphique donnant la vitesse du véhicule en fonction du temps. (3 points)
2. Calculez la distance parcourue par le véhicule après 4 s, 8 s et 12 s. (3 points)
3. Calculez la vitesse moyenne du véhicule sur tout le trajet. (2 points)

Problème 3 (5 points)

Un bateau dont la cheminée culmine à 28 m d’altitude quitte le port. Un observateur resté sur le quai observe le bateau qui s’éloigne à la vitesse de 23 noeuds (1 noeud = 1 mille marin par heure, soit 0.514 m/s).

1. Exprimez la distance franchie par le bateau lorsque sa cheminée disparaît à l’horizon. (2 points)
2. Calculez cette distance en utilisant la valeur a=6370 km pour le rayon terrestre. (1 point)
3. Combien de temps après le départ du bateau cette disparition se produit-elle ? (2 points)

Problème 4 (6 points)

Une bille de plastiline de masse m se déplace à 5 m/s. Une seconde bille de masse 2m heurte la première et se colle à elle. Le système final a une vitesse de même grandeur que la première bille (5 m/s) mais de direction perpendiculaire.

1. Donnez les équations postulant la conservation de la quantité de mouvement selon Ox et Oy. (2 points)
2. Calculez l’angle formé par la vitesse de la seconde bille avant le choc. (2 points)
3. Calculez la grandeur de la vitesse de la seconde bille avant le choc. (2 points)

Résultats