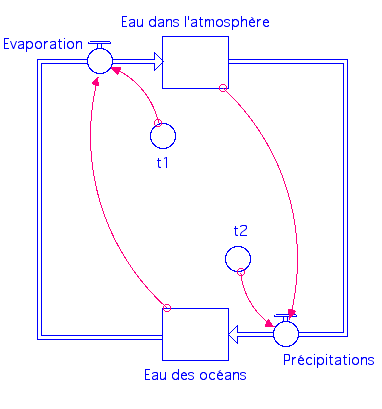
Construction d’un modèle de cycle à partir d’une description verbale.
Un cycle peut être représenté de différentes manières. Le modèle proposé devrait permettre de dégager les propriétés principales des cycles et d’expliciter le rôle joué par les paramètres retenus.

Tableau des notions et des activités
Présentation
Objectifs de l’activité
– construire un modèle
– formuler des hypothèses
– identifier les grandeurs et phénomènes pertinents
– proposer une représentation des grandeurs et phénomènes retenus
– simuler une évolution
– utiliser des relations de proportionnalité
Notions
– cycle
– modèle
– représentation
– schématisation
Matériel
– ordinateur, logiciel Stella
Durée
– 2 fois 45 minutes
Activités
Description
L’évaporation de l’eau des océans produit du gaz d’eau. En se liquéfiant, ce gaz donne lieu à de très fines gouttelettes qui forment les nuages. Lorsque les gouttelettes se réunissent et que leur taille augmente, elles tombent et finissent par retourner à l’océan.
Questions
- Pourquoi peut-on assimiler cette description à un cycle ?
- Dans quels différents états l’eau apparaît-elle dans ce cycle ?
- Quelles sont les changements d’état mentionnés dans la description ?
- Quels sont les facteurs principaux qui conditionnent ces changements d’état ? Quelles hypothèses faites-vous ?
Activités
– Construisez une représentation du cycle faisant apparaître :
- les grandeurs retenues
- les changements d’état
- les relations postulées
– Formulez explicitement les relations envisagées.
– Proposez des valeurs numériques caractérisant les grandeurs retenues.
– Pronostiquez l’évolution d’une ou de plusieurs grandeurs pour :
- différents jeux de valeurs initiales
- différentes valeurs des paramètres
– Simulez cette évolution et comparez-là à vos prévisions.
– Commentez l’éventuel désaccord entre l’évolution observée et votre pronostic.
– Téléchargez le fichier joint, ouvrez-le [1] et répondez aux questions suivantes :
- Que représentent les différentes lignes horizontales sur le graphique ?
- La situation représentée correspond-elle à un cycle ?
- Quelles valeurs (autres que 0) faut-il attribuer aux paramètres :
- évaporation
- liquéfaction
- précipitations
pour obtenir 3 lignes horizontales, comme sur la figure de départ ?
À l’attention du maître
Représentation schématique
Définir des relations
Simuler une évolution
Résumé des étapes du calcul
Les paramètres du modèle
Temps de résidence de l’eau dans les différents états
- La description peut être assimilée à un cycle car elle ne mentionne ni source (création d’eau) ni puits (disparition d’eau).
- L’eau apparaît, dans la description, sous forme liquide et gazeuse.
- Deux changements d’état sont mentionnés : l’évaporation et la liquéfaction.
- Pour construire un modèle simple, nous supposerons que :
- l’évaporation ne dépend que de la température (qui dépend, elle, de la couverture nuageuse)
- la liquéfaction est uniquement conditionnée par la quantité de gaz d’eau présente dans l’atmosphère
- les précipitations dépendent de la masse nuageuse.
Représentation schématique du cycle
Nous utilisons des « réservoirs » pour représenter l’eau des océans, les gaz d’eau et les nuages. L’évaporation, la liquéfaction et les précipitations sont représentées par des « flux » munis de vannes. Ces flux indiquent le sens de transfert entre les réservoirs.

Relations postulées
Les relations sont signalées par des « liens ». Ces relations sont à lire de la manière suivante : l’élément qui est à l’origine d’un lien agit sur celui qui se trouve à son extrémité. Le lien symbolise une relation « causale ».
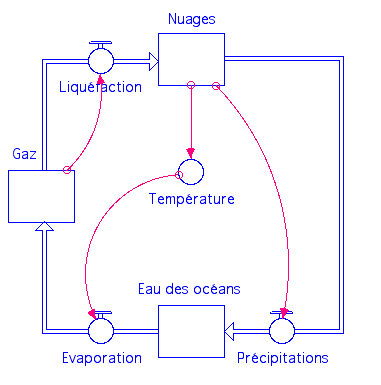
N. B. Il n’est pas possible de faire aboutir un lien sur un réservoir : pour agir sur un réservoir, il faut utiliser un flux.
Lorsqu’il s’agit d’envisager des relations, il faut plutôt brimer l’imagination des élèves - qui sont volontiers adeptes du « tout agit sur tout et réciproquement » - que l’encourager. Mais lorsqu’il faut définir - à l’aide d’égalités - les relations postulées, il faut les aider ! Nous pouvons par exemple commencer par leur demander :
- le type de dépendance (fonction croissante ou décroissante)
- de donner l’allure graphique des dépendances, en n’utilisant que des droites, lorsqu’on reporte sur l’axe horizontal la grandeur située à l’origine du lien et sur l’axe vertical celle se trouvant à son extrémité
- de proposer une étendue pour chaque axe
- éventuellement d’établir l’équation des droites.
Pour les relations postulées nous avons les allures et les définitions suivantes :
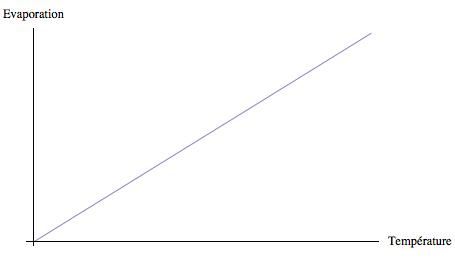
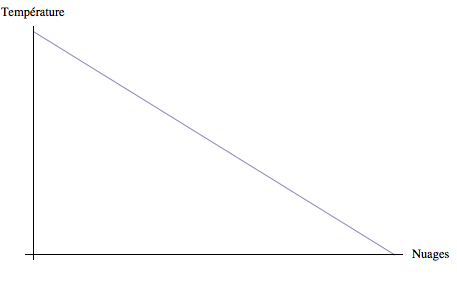
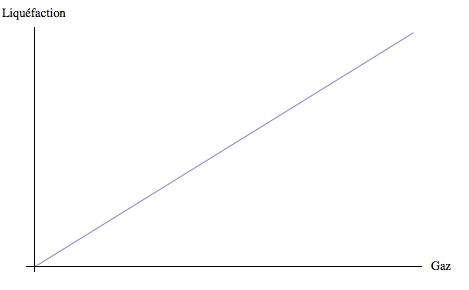
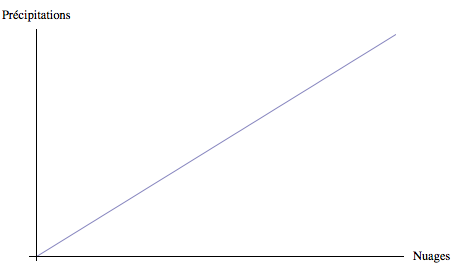
Les différentes constantes de proportionnalité peuvent être représentées par de petits cercles dans le schéma :
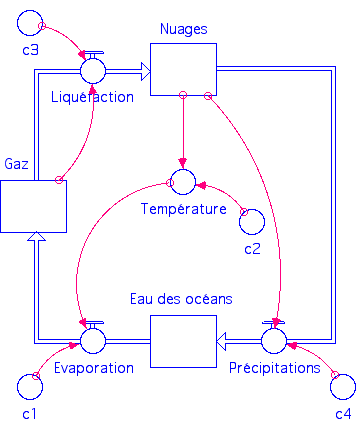
La schématisation précédente clarifie la description initiale en mettant en évidence les grandeurs importantes ainsi que les relations qu’elles entretiennent. Mais elle ne permet pas encore d’obtenir l’évolution temporelle de ces grandeurs pour différentes valeurs des « paramètres » (dans ce modèle, ce sont les constantes c1, c2, c3 et c4 qui joueront le rôle de paramètres). Pour simuler une évolution, il faut obtenir, à partir de valeurs initiales, la valeur de chaque grandeur à chaque instant lorsque le temps s’écoule.
Valeurs initiales
Elles doivent être précisées pour chaque réservoir. Si on ne connaît pas la quantité totale d’eau présente dans le cycle (environ 1.4 × 1018 tonnes), on peut travailler avec des valeurs relatives exprimées en %: on indiquera par exemple 85 pour le réservoir « Eau des océans », 10 pour le réservoir « Gaz » et 5 pour le réservoir « Nuages ». Les valeurs des constantes de proportionnalité sont comprises entre 0 et 1.
Calcul des valeurs d’instant en instant
La simulation peut commencer [2]. Le calcul des valeurs, d’instant en instant, peut se faire à la main. Les seules opérations qu’il fait intervenir sont les quatre opérations élémentaires de l’arithmétique, comme on peut le constater en examinant les équations ci-dessous : [3]
Eau_des_océans(t) = Eau_des_océans(t - dt) + (Précipitations - Evaporation) * dt
INIT Eau_des_océans = 85
INFLOWS:
Précipitations = c4*Nuages
OUTFLOWS:
Evaporation = c1*Température
Gaz(t) = Gaz(t - dt) + (Evaporation - Liquéfaction) * dt
INIT Gaz = 10
INFLOWS:
Evaporation = c1*Température
OUTFLOWS:
Liquéfaction = c3*Gaz
Nuages(t) = Nuages(t - dt) + (Liquéfaction - Précipitations) * dt
INIT Nuages = 5
INFLOWS:
Liquéfaction = c3*Gaz
OUTFLOWS:
Précipitations = c4*Nuages
c1 = .1
c2 = 1
c3 = .25
c4 = .5
Température = 30-c2*NuagesCe calcul est long et fastidieux ! Il n’est pas question de le faire exécuter par les élèves : le recours à l’informatique s’impose ! Mais il est important que les élèves comprennent auparavant les étapes du calcul qui se résument à :
- découper le temps en intervalles (pas d’intégration dt)
- obtenir la valeur numérique d’un réservoir au temps t à partir de sa valeur au temps précédent t-dt en lui ajoutant la contribution nette des flux (entrants moins sortants)
- maintenir constante la valeur des flux durant l’intervalle dt.
Faire varier les paramètres du modèle
L’intérêt d’une simulation, c’est de pouvoir examiner différentes évolutions dans un laps de temps beaucoup plus court que celui requis par une expérimentation. Simuler, c’est comprimer l’espace et le temps tout en offrant la possibilité d’étendre la compréhension ! Le logiciel Stella, idéal pour apprendre à modéliser, offre de très intéressantes possibilités pour faire varier les paramètres d’un modèle. Mais, en termes d’interaction entre l’utilisateur et le modèle, il existe encore mieux. Le logiciel Mathematica permet, dès la version 6, la réalisation d’interfaces d’une très grande simplicité d’usage.
Temps de résidence de l’eau dans les différents états
Si on connaît les parts relatives d’eau (en % par exemple) dans les différents réservoirs, on peut trouver le rapport des temps de résidence de l’eau dans ces réservoirs :
$\frac{\emph{\text{Part d’eau dans l’atmosphère}}}{\emph{\text{Part d’eau des océans}}}=\frac{t_2}{t_1}$
En supposant que l’eau du cycle (environ 1.4 × 1018 tonnes) se répartit entre les océans et l’atmosphère et en admettant que la part des océans représente le 99.9999 % du total, il est possible, si on connaît la quantité annuelle d’eau évaporé (4 × 1014 tonnes/an), d’estimer les précipitations annuelles ainsi que les temps caractéristiques de résidence de l’eau dans l’océan et dans l’atmosphère à l’aide d’un modèle très simple :