
Équations différentielles ordinaires : quelques définitions. Solution générale d’une équation. Conditions initiales et valeurs aux limites. Solutions particulières.
par bernard.vuilleumier
Résoudre une équation différentielle revient à trouver une fonction qui est continue sur un intervalle et qui possède toutes les dérivées qui sont présentes dans l’équation. La solution générale d’une équation différentielle est une famille de courbes qui dépendent de constantes arbitraires. Les conditions initiales ou les conditions aux limites permettent de déterminer les valeurs de ces constantes d’intégration et de trouver des solutions particulières.
Équations différentielles ordinaires
Une équation différentielle est une équation qui contient la dérivée d’une ou de plusieurs fonctions dépendant d’une ou de plusieurs variables indépendantes. Si l’équation ne contient que des dérivées par rapport à une seule variable indépendante, l’équation est appelée équation différentielle ordinaire.
Questions
Quelles sont les équations, parmi les exemples ci-dessous, qui sont des équations différentielles ordinaires ?
- $\frac{dy}{dx}=\frac{x^2}{y^2cos(y)}$
- $\frac{dy}{dx}+\frac{du}{dx}=u+x^2y$
- $(y-1)dx+xcos(y)dy=0$
- $\frac{\partial u}{\partial t}=\frac{\partial ^2 u}{\partial x^2}$
- $x^2y’’+xy’+(x^2-n^2)y=0$
- $\frac{\partial ^2 u}{\partial t^2}=\frac{\partial ^2 u}{\partial x^2}$
Lorsqu’une équation contient des dérivées partielles d’une ou de plusieurs fonctions, l’équation est appelée équation différentielle aux dérivées partielles. Ces équations jouent un rôle très important en physique.
Ordre d’une équation différentielle
Les équations différentielles peuvent être classées selon différents critères. La première classification consiste à distinguer entre équations différentielles ordinaires (fréquemment désignées par l’abréviation EDO dans les ouvrages francophones et par ODE dans les ouvrages anglophones) et équations différentielles aux dérivées partielles (EDP, PDE). Cette classification peut être affinée avec la définition suivante : la dérivée la plus élevée (première,…,$n^e$) figurant dans l’équation donne l’ordre de cette dernière.
Questions
Quel est l’ordre de chacune des équations différentielles suivantes ?
- $\frac{dy}{dx}=\frac{x^2}{y^2cos(y)}$
- $u_{xx}+u_{yy}=0$
- $(y-1)dx+xcos(y)dy=0$
- $(\frac{dy}{dx})^4=y+x$
- $y^3+\frac{dy}{dx}=1$
Équations différentielles linéaires
Une équation différentielle d’ordre n est linéaire si elle a la forme suivante :
$a_n(x)\frac{d^n y}{dx^n}$+$a_{n-1}(x)\frac{d^{n-1}y}{dx^{n-1}}$+ … +$a_2(x)\frac{d^2y}{dx^2}$+$a_1(x)\frac{dy}{dx}$+$a_0 (x)y=f(x)$
où les fonctions $a_j(x)$, $j$= 0, 1, … n et $f(x)$ sont données.
Questions
Quelles sont, parmi les équations suivantes, celles qui sont linéaires :
- $\frac{dy}{dx}=x^3$
- $\frac{d^2u}{dx^2}+u=e^x$
- $(y-1)dx+xcos(y)dy=0$
- $\frac{d^3y}{dx^3}+y\frac{dy}{dx}=x$
- $\frac{dy}{dx}+x^2y=x$
- $\frac{d^2x}{dt^2}+sin(x)=0$
Résoudre une équation différentielle ordinaire linéaire avec Mathematica
Mathematica peut résoudre des équations différentielles ordinaires linéaires de n’importe quel ordre si elles ont des coefficients constants. Il peut aussi résoudre plusieurs équations linéaires jusqu’à l’ordre 2 lorsque les coefficients ne sont pas constants.
Solution générale d’une équation
– Équation ordinaire linéaire du premier ordre
Considérons l’équation $\frac{dy}{dt}=a t+v_0$ qui exprime la vitesse d’un mobile selon l’axe y lorsqu’il est soumis à une accélération a constante. Résolvons cette équation avec Mathematica :
La solution générale est une famille de courbes définies par :
$y(t)=\frac{1}{2}at^2+v_0t+C[1]$
À chaque valeur de la constante d’intégration C[1] correspond une courbe :
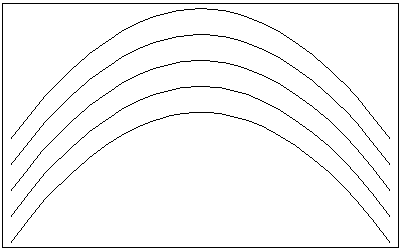
La solution générale correspond à une famille de courbes. Chaque courbe est une solution particulière.
– Équation ordinaire linéaire du second ordre
Considérons une masse accrochée à un ressort. Résolvons l’équation différentielle décrivant le mouvement de la masse :
La solution générale comporte deux constantes d’intégration C[1] et C[2] :
$y(t)=C[1]cos(\sqrt\frac{k}{m}t)+C[2]sin(\sqrt\frac{k}{m}t)$
Lorsque nous disposons de conditions pour un même temps, nous parlons de problème à valeurs initiales. Si nous connaissons la position initiale de la masse, nous pouvons trouver la constante C[1]. Substituons la valeur 0 pour t dans la solution générale y(t) :
Nous obtenons C[1]. Comme y(0)=0, nous en déduisons que la constante C[1] vaut 0. Si nous connaissons la vitesse initiale, nous pouvons trouver la constante C[2]. Dérivons la fonction y(t) par rapport au temps pour obtenir la vitesse et posons t=0 :
Il vient $\sqrt\frac{k}{m}C[2]$. Comme la vitesse au temps t=0 vaut 1, nous en déduisons que $C[2]=\sqrt\frac{m}{k}$. La solution particulière correspondant à ces conditions initiales est donc :
$y(t)=\sqrt\frac{m}{k}sin(\sqrt\frac{k}{m}t)$
Conditions aux limites
Lorsque nous disposons de conditions pour des temps différents nous parlons de problème à valeurs aux limites. Si nous connaissons la position initiale y(0)=0 et la position en t=1/4 s, y(1/4)=1/10 m par exemple, nous pouvons trouver les constantes d’intégration C[1] et C[2]. En substituant la valeur 0 pour t dans la solution générale y(t), nous obtenons, comme précédemment C[1]=0. En substituant la valeur 1/4 s pour t, dans y(t) :
Il vient C[2]. Nous en déduisons que C[2] vaut 1/10 m. La solution particulière correspondant à ces conditions aux limites est donc :
$y(t)=\frac{1}{10}sin(\sqrt\frac{k}{m}t)$
Représentons cette solution pour m=1 kg et k=4$\pi^2 m$ N/m :
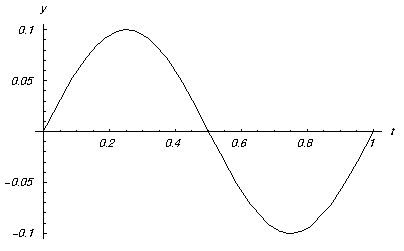
En donnant d’emblée les conditions initiales, nous obtenons bien sûr la même solution particulière :
Conclusion
Mathematica vous permet de résoudre des équations différentielles ordinaires linéaires à coefficients constants de n’importe quel ordre. La solution générale d’une équation différentielle ordinaire comporte autant de constantes d’intégration que l’ordre de l’équation. En substituant les conditions initiales ou les conditions aux limites dans la solution générale, vous pouvez déterminer la valeur de ces constantes d’intégration et trouver des solutions particulières. Ces dernières peuvent aussi être obtenues en spécifiant d’emblée les conditions initiales ou les valeurs aux limites lors de la résolution de l’équation.