4 problèmes : orbite circulaire basse, période de révolution, champ de pesanteur à l’intérieur et à l’extérieur d’une planète, conservation du moment cinétique.
– Champ : gravitation et moment cinétique
– Documents autorisés : Tables CRM. Calculette.
– Vendredi 25 mai 2007, CECNB, M3-M4, 95 min.
– Moyenne de classe : 4.10
– Écart type : 1.15
– Effectif : N=15
Problème 1
Un satellite, qui orbite sur un cercle à très basse altitude autour d’une planète sans atmosphère, a une période T.
- Exprimez la masse volumique de cette planète à partir de T.
- Peut-on exprimer le rayon de la planète à partir de T ? Justifiez votre réponse !
- Calculez cette masse volumique si T=84 minutes.
Problème 2
On imagine un tunnel rectiligne suivant un diamètre de la Lune.
Exprimez l’accélération de la pesanteur à une distance r du centre de la Lune dans les deux cas suivants :
- r est inférieur au rayon R de la Lune.
- r est supérieur au rayon R de la Lune.
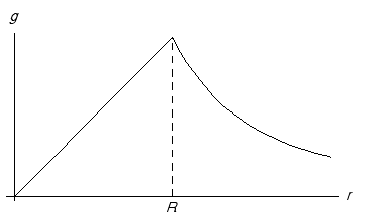
- Représentez graphiquement cette accélération en fonction de r.
On lâche un objet de masse m depuis la surface dans ce tunnel.
- Exprimez le temps T d’aller retour de l’objet (période).
- Calculez cette période d’oscillation.
Problème 3
On place un satellite en orbite circulaire autour d’une planète de masse M et de rayon R. On observe que sa période de révolution vaut T.
- Exprimez à partir de ces données l’altitude h à laquelle il se trouve.
- Calculez cette altitude pour la Terre et pour des périodes de 2 et 4 h.
Problème 4
Un mobile se déplace selon la trajectoire suivante :
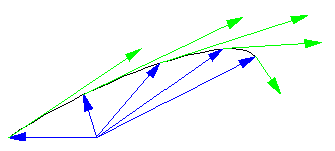
L’angle entre le vecteur position et le vecteur quantité de mouvement lorsque les deux vecteurs sont issus du même point vaut respectivement, pour les positions successives dessinées : 140.3, 82.2, 31.3, 31.3 et 82.6 °.
- Calculez la grandeur du moment cinétique pour chacune de ces positions.
- Ce déplacement est-il compatible avec un champ de forces centrales ? Justifiez votre réponse !
Corrigé
Problème 1 (6 points)
En égalant la force de gravitation à une force centripète et en exprimant la masse M de la planète à l’aide de son volume V et de sa masse volumique $\rho$, on obtient une équation qu’il est possible de résoudre par rapport à $\rho$. On trouve :
La relation qui lie $\rho$ à T ne comporte pas le rayon R de la planète. Il n’est donc pas possible d’exprimer ce dernier uniquement à partir de $\rho$ et de T.
En introduisant les valeurs numériques de la constante de la gravitation universelle G et de la période T, dans l’expression donnant $\rho$, on obtient :
Problème 2 (10 points)
L’accélération g à l’intérieur du tunnel ne dépend que de la masse $M_{int}$ comprise dans une sphère dont le rayon est donné par la position r du mobile $g=\frac{GM_{int}}{r^2}$. En exprimant $GM_{int}$ à l’aide de M, de R et de r, $M_{int}=\frac{r^3}{R^3}M$, on peut écrire $g=\frac{GM}{R^3}r$. Cette expression montre que l’accélération à l’intérieur du tunnel est proportionnelle à r.
Lorsque r > R, l’accélération g est donnée par $g=\frac{GM}{r^2}$
La représentation graphique de g en fonction de r a, pour une planète de rayon R, l’allure suivante :
Comme l’accélération $g=\frac{GM}{R^3}r$ du mobile à l’intérieur du tunnel est proportionnelle à l’écart r par rapport à sa position d’équilibre (milieu du tunnel), il s’agit d’un oscillateur harmonique. La constante de rappel k est donnée par $k=\frac{F}{r}=\frac{mg}{r}=\frac{GM}{R^3}$ et la période par $T=2\pi\sqrt\frac{m}{k}$. Elle vaut donc :
En introduisant les données numériques dans cette expression, on obtient T=6500 s.
Problème 3 (6 points)
Ici de nouveau, il faut égaler la force de gravitation à une force centripète, puis simplifier l’expression :
En résolvant par rapport à h, on obtient :
En introduisant les données numériques, on obtient les hauteurs suivantes : 1.69$\times$106 m et 6.42$\times$106 m.
Problème 4 (6 points)
En mesurant la longueur du vecteur position $\vec r$ et du vecteur quantité de mouvement $m\vec v$, on peut calculer la grandeur du moment cinétique $\vec L$ à l’aide de l’expression :
On trouve, aux erreurs de mesures près, un moment cinétique constant.
Ce moment cinétique constant est compatible avec un champ de forces centrales.
