Cette activité permet de découvrir les notions d’attracteur et de figure fractale avec une feuille de papier, un dé, une règle, un compas et un mode opératoire (règles du jeu). En proposant une observation du jeu sans en donner les règles, il est aussi possible de réaliser une activité exploratoire visant à découvrir ces règles.

Objectifs
– représenter
– conjecturer
– interpréter
– observer
– exercer l’esprit critique

Notions
– hasard et déterminisme
– milieu d’un segment (construction au compas)
– itinéraire chaotique
– attracteur
– figure fractale

Durée
– 2 fois 45 minutes

Description

Vous allez jouer au jeu du chaos ! Pour jouer à ce jeu, il vous faut une feuille de papier, un crayon, un compas, une règle et un dé. Dessinez un triangle équilatéral sur la feuille de papier et numérotez les sommets de 1 à 3. Choisissez arbitrairement un point $P_0$ sur votre feuille. Tirez au hasard, à l’aide du dé, un des sommets du triangle. Reliez $P_0$ à ce sommet et placez, au milieu du segment ainsi obtenu, le point $P_1$. Tirez au hasard un des sommets du triangle. Reliez $P_1$ à ce sommet et placez, au milieu du segment ainsi obtenu, le point $P_2$, et ainsi de suite.

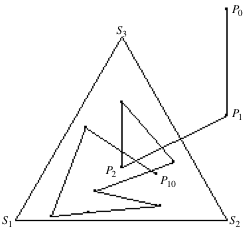
Questions

1. À votre avis, peut-on prévoir :

• où les points se placeront après quelques tirages
• l’itinéraire qu’on obtiendra en reliant les points successifs obtenus.

2. Existe-t-il des régions dans lesquelles il n’y aura pas de point ?
3. La répartition des points est-elle modifiée si l’on part d’un autre point initial ?

Activités

1. Dessinez un triangle équilatéral sur une grande feuille de papier
2. Choisissez n’importe où un point sur la feuille
3. Tirez au hasard un des sommets du triangle
4. Reliez le point au sommet obtenu et prenez le milieu de ce segment
5. Tirez à nouveau un sommet au hasard
6. Reliez le dernier point à ce sommet et prenez le milieu du segment
7. Continuez le processus aussi longtemps que vous en aurez le loisir !

Extension

Ceux qui voudraient utiliser un ordinateur pour obtenir plus de points peuvent définir la séquence de points $P_1$, …, $P_n$ en répétant n fois les instructions suivantes :

• tirer au hasard un des sommets du triangle
• relier le point précédent $P_n$ à ce sommet
• placer au milieu du segment ainsi obtenu le point suivant $P_{n+1}$
• répéter les opérations ci-dessus.

A l’attention du maître

Réponses aux questions

1. La répartition des points est totalement prévisible. Ils convergent vers un attracteur (motif de Sierpinski). Le processus est équivalent à un système de fonctions itérées (IFS) défini par trois transformations affines contractantes qui forment un opérateur. Hutchinson a démontré, pour ce type d’opérateur, l’existence et l’unicité d’un attracteur (J. E. Hutchinson, « Fractals and self-similarity », Indiana Univ. Math Journal, 30, 1981, pp. 713-747).

L’itinéraire obtenu en reliant les points successifs en revanche est totalement imprévisible, ce qui signifie que l’on ne peut pas prévoir à l’avance où se situera tel ou tel point, bien que la répartition globale des points soit parfaitement connue !
2. Oui, il existe des régions dans lesquelles il n’y aura plus aucun point après quelques tirages, et elles sont faciles à construire : la région centrale obtenue en prenant le milieu de chaque côté du triangle et en reliant ces milieux ne comportera, après quelques tirages, plus aucun point. Et, chose plus surprenante encore, toutes les régions définies par ce procédé, sur n’importe quel triangle ne comporteront aucun point !
3. La répartition des points ne dépend pas du point initial, et on obtient encore une répartition similaire si on part d’un triangle quelconque.

Extension

La simulation donnée en document joint permet de constater que la position de chaque point est due en partie au hasard en partie à des règles. Elle peut servir de point de départ d’une approche exploratoire qu’on peut stimuler par des questions du type :

• Quand et comment le hasard intervient-il ?
• Quelles sont les règles régissant le passage d’un point au suivant ?
• Pourquoi un point est-il de telle ou telle couleur ?
• L’itinéraire obtenu en reliant les points présente-t-il des régularités ?
• La répartition des points forme-t-elle un motif ?
• Du hasard et du déterminisme lequel finit par l’emporter ? Pourquoi ?
  Chaotic Itinerary but Regular Pattern from the Wolfram Demonstrations Project by Bernard Vuilleumier

  Sujets liés

Sur OWL Math & Sciences
– L’attracteur d’un photocopieur
– Triangle de Sierpinski

From Wolfram Demonstrations Project
– Chaotic Itinerary but Regular Pattern
– Attractors of Iterated Affine Transform Systems
– Fractal Creation with Iterated Function Systems
– Sierpinski Sieve

From MathWorld—A Wolfram Web Resource
– Weisstein, Eric W. « Chaos Game. »

Wolfram Demonstrations Project : mode d’emploi