
Cartes, relations et modèles Stella. Comportements génériques. Dynamique. Oscillateurs.
Problème 1
– Par quel élément de Stella (stock ou flux) représenteriez-vous les grandeurs suivantes :
| Grandeur | Élément Stella | Grandeur | Élément Stella |
|---|---|---|---|
| Population | Vitesse | ||
| Intérêts annuels | Fatigue | ||
| Distance parcourue | Travail journalier | ||
| Décès mensuels | Volume | ||
| Dette | Débit |
– Dessinez les cartes des modèles les plus simples possibles donnant lieu aux comportements ci-dessous et donnez les relations qui définissent les flux et les valeurs initiales pour chaque modèle.

– Construisez deux modèles - les plus simples possibles - l’un donnant l’évolution ci-dessous à gauche, l’autre l’évolution ci-dessous à droite et donnez une interprétation de chacun de ces modèles (en attribuant par exemple un nom significatif à chaque élément des modèles).
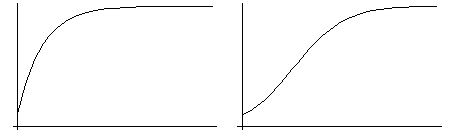
Problème 2
Vous lancez un ballon de 30 cm diamètre verticalement vers le haut à la vitesse de 20 m/s. La masse du ballon vaut 300 g et son coefficient de forme Cx 0.3. Il subit une force de frottement proportionnelle au carré de sa vitesse (masse volumique de l’air : 1.29 kg/m3).
– Quelle hauteur le ballon atteint-il ?
– Quel temps lui faut-il pour atteindre cette hauteur ?
– Combien de temps lui faut-il pour regagner son point de départ ?
d) Comment les réponses aux points 1, 2 et 3 sont-elles modifiées si le ballon ne subit aucune force de frottement ?
Problème 3
Un constructeur fournit les données suivantes pour une voiture :
| Caractéristiques techniques | |
|---|---|
| Puissance | 325 chevaux |
| Vitesse maximale | 275 km/h |
| Longueur | 443 cm |
| Largeur | 180 cm |
| Hauteur | 131 cm |
| Cx | 0.29 |
| Poids | 1650 kg |
– Calculez le temps nécessaire à cette voiture pour :
- atteindre la vitesse de 100 km/h
- atteindre la vitesse de 160 km/h
- franchir 400 m départ arrêté
- franchir 1000 m départ arrêté.
Problème 4
Vous accrochez une masse m de 1 kg à un ressort de raideur k=9.87 N/m. La position initiale de la masse correspond à l’extrémité libre du ressort « à vide » qui coïncide avec l’origine de l’axe (x0=0). La vitesse initiale de la masse est nulle.
– Que vaut la période de cet oscillateur ?
– Que doit valoir x0 pour que la masse reste en équilibre ?
– Que doit valoir la longueur l d’un pendule pour qu’il ait la même période s’il oscille avec une amplitude de 30° ?
N. B. N’oubliez pas d’indiquer, pour chacun des problèmes, la méthode et le pas d’intégration utilisés.
